7 класс Онлайн

§ 7. Координатная плоскость

1. Оси координат и отыскание координат точки на плоскости

На координатной прямой «прописаны» точки-жильцы, у каждой точки есть свой номер дома — её координата. Если же точка берётся в плоскости, то для её «прописки» нужно указывать не только номер дома, но и номер квартиры. Напомним, как это делается.

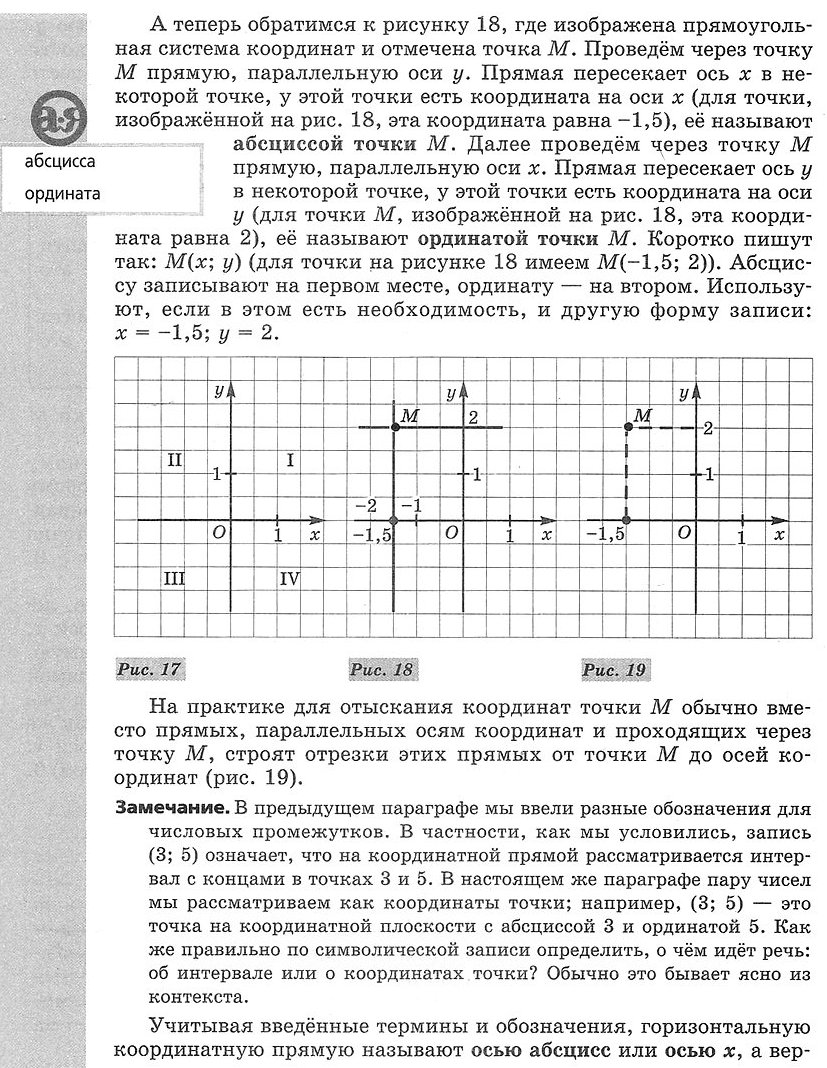
Проведём две взаимно перпендикулярные координатные прямые и будем считать началом отсчёта на обеих прямых точку их пересечения — точку О. Тем самым на плоскости задана прямоугольная система координат (рис. 17), которая превращает обычную плоскость в координатную. Точку О называют началом координат, координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами. Координатные углы нумеруют так, как показано на рисунке 17.

А теперь обратимся к рисунку 18, где изображена прямоугольная система координат и отмечена точка М. Проведём через точку М прямую, параллельную оси у. Прямая пересекает ось х в некоторой точке, у этой точки есть координата на оси х (для точки, изображённой на рис. 18, эта координата равна -1,5), её называют абсциссой точки М. Далее проведём через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата на оси у (для точки М, изображённой на рис. 18, эта координата равна 2), её называют ординатой точки М. Коротко пишут так: М(х; у) (для точки на рисунке 18 имеем М(-1,5; 2)). Абсциссу записывают на первом месте, ординату — на втором. Используют, если в этом есть необходимость, и другую форму записи: х = -1,5; у = 2.

На практике для отыскания координат точки М обычно вместо прямых, параллельных осям координат и проходящих через точку М, строят отрезки этих прямых от точки М до осей координат (рис. 19).

Замечание. В предыдущем параграфе мы ввели разные обозначения для числовых промежутков. В частности, как мы условились, запись (3; 5) означает, что на координатной прямой рассматривается интервал с концами в точках 3 и 5. В настоящем же параграфе пару чисел мы рассматриваем как координаты точки; например, (3; 5) — это точка на координатной плоскости с абсциссой 3 и ординатой 5. Как же правильно по символической записи определить, о чём идёт речь: об интервале или о координатах точки? Обычно это бывает ясно из контекста.

Учитывая введённые термины и обозначения, горизонтальную координатную прямую называют осью абсцисс или осью х, а вертикальную координату …

Именно так мы и действовали, находя координаты точки М на рисунке 18.

Если точка Mi(x; у) принадлежит первому координатному углу, то х > 0, у > 0; если точка Мг(л:; у) принадлежит второму координатному углу, то х < 0, у > 0; если точка М3(х; у) принадлежит третьему координатному углу, то х < 0, у < 0; если точка Mi(x; у) принадлежит четвёртому координатному углу, то х > 0, у < 0 (рис. 21).

А что будет, если точка, координаты которой надо найти, лежит на одной из осей координат? Пусть точка А лежит на оси х, а точка В — на оси у (рис. 22). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, её координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси х: сама ось х пересекает ось у в точке О с координатой (ординатой) 0.

В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; -1,5). А для точки О имеем 0(0; 0).

Вообще любая точка на оси х имеет координаты (х; 0), а любая точка на оси у — координаты (0; у).

2. Построение точки на плоскости по её координатам

Выше мы обсудили, как находить координаты точки на координатной плоскости. А как решать обратную задачу, т. е. как, задав координаты, построить соответствующую точку? Чтобы выработать алгоритм, проведём два вспомогательных, но в то же время важных рассуждения.

Первое рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси у и пересекающая ось х в точке с координатой (абсциссой) 4 (рис. 23). Любая точка, лежащая на этой прямой, имеет абсциссу 4. Так, для точек Мь М2, М3 имеем Мх(4; 3), М2(4; 6), М3(4; -2). Иными словами, абсцисса любой точки М прямой I удовлетворяет условию х = 4. Если же взять точку, не лежащую на этой прямой, то её абсцисса будет отлична от 4. Говорят, что х = 4 — уравнение прямой I или что прямая I (и только она) удовлетворяет уравнению х = 4.

На рисунке 24 изображены прямые, удовлетворяющие уравнениям х — -4 (прямая 1\), х = — 1 (прямая Z2), х = 3,5 (прямая 13). А какая прямая удовлетворяет уравнению х = 0? Догадались? Ось у.

Второе рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси х и пересекающая ось у в точке с координатой (ординатой) 3 (рис. 25). Любая точка, лежащая на этой прямой, имеет ординату 3. Так, для точек Мь М2, М3 имеем: МД0; 3), М2(4; 3), М3(-2; 3). Иными словами, ордината любой точки М прямой I удовлетворяет условию у = 3. Если же взять точку, не лежащую на этой прямой, то её ордината будет отлична от 3. Говорят, что у = 3 — уравнение прямой I или что прямая I (и только она) удовлетворяет уравнению у — 3.

На рисунке 26 изображены прямые, удовлетворяющие уравнениям у = -4 (прямая 1{), у = -1 (прямая Z2)> г/ = 3,5 (прямая 13). А какая прямая удовлетворяет уравнению у = 0? Догадались? Ось х.

Заметим, что математики, стремясь к краткости речи, говорят «прямая х = 4», а не «прямая, удовлетворяющая уравнению х = 4». Аналогично они говорят «прямая у = 3», а не «прямая, удовлетворяющая уравнению у = 3». Мы будем поступать точно так же.

Подведём итоги.

Чтобы построить на координатной плоскости хОу прямую х — а, нужно:

• 1) отметить на оси х точку с абсциссой а;
• 2) провести через неё прямую, параллельную оси у.

Чтобы построить на координатной плоскости хОу прямую у = b, нужно:

• 1) отметить на оси у точку с ординатой b;
• 2) провести через неё прямую, параллельную оси х.

Вернёмся теперь к рисунку 18. Обратите внимание, что точка М(-1,5; 2), которая там изображена, есть точка пересечения прямой х = -1,5 и прямой у = 2. Теперь, видимо, будет понятен алгоритм построения точки по заданным её координатам.

Алгоритм построения точки М(а; b) в прямоугольной системе координат хОу

1. Построить прямую х = а.
2. Построить прямую у = b.
3. Найти точку пересечения построенных прямых — это и будет точка М(а; b).

ПРИМЕР 1. В системе координат хОу построить точки: А(1; 3), В(-2; 1), С(4; 0), D(0; -3).

Решение: Точка А есть точка пересечения прямых х = 1 и у = 3 (рис. 27). Точка В есть точка пересечения прямых х — -2 и у = 1. Точка С принадлежит оси х, а точка D — оси у.

Рене Декарт (1596—1650), французский философ, математик, физик, физиолог.

Впервые прямоугольную систему координат на плоскости стал активно использовать Рене Декарт для решения геометрических задач алгебраическими методами и, обратно, для замены алгебраических моделей геометрическими. Поэтому иногда говорят: «декартова система координат», «декартовы координаты».

ПРИМЕР 2. В координатной плоскости хОу дана точка М(3; 2). Построить точку, симметричную точке М: а) относительно оси х; б) относительно оси у, в) относительно начала координат. Указать координаты построенных точек.

Решение: а) Точка М(3; 2) указана на рисунке 28 — это точка пересечения прямых х = 3, у = 2. Точка Р симметрична точке М относительно оси х, её координаты таковы: Р(3; -2). Обратите внимание: абсцисса осталась прежней, а знак ординаты изменился.

б) Точка N симметрична точке М относительно оси у, её координаты таковы: N(~3; 2). Обратите внимание: ордината осталась прежней, а знак абсциссы изменился.

в) Точка К симметрична точке М относительно начала координат, её координаты таковы: К(-3; -2). Обратите внимание: изменились знаки обеих координат.

Вопросы для самопроверки

1. Что такое прямоугольная система координат на плоскости?
2. Сформулируйте алгоритм отыскания координат точки М, заданной в системе координат хОу.
3. В какой четверти координатной плоскости хОу находится точка М(х; у), если: а) х < 0, у > 0; б) х > 0, у < 0; в) х < 0, у < 0; г) х > 0, у > 0?

4. Как на координатной плоскости хОу построить прямую: а) х = а; б) у = b?

5. Какая прямая в координатной плоскости хОу задаётся уравнением: а) х = 0; б) у = 0?

6. Сформулируйте алгоритм построения точки М(а; b) в прямоугольной системе координат хОу.
7. Как на координатной плоскости расположены друг относительно друга точки: М{а; b) и Р(а; -b); М(а; b) и N(-a; b); М(а; b) и К(-а; -b)?