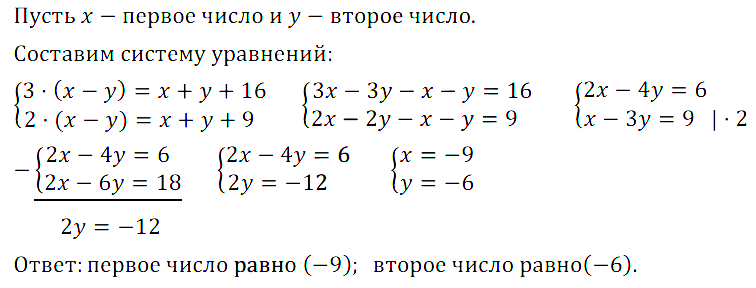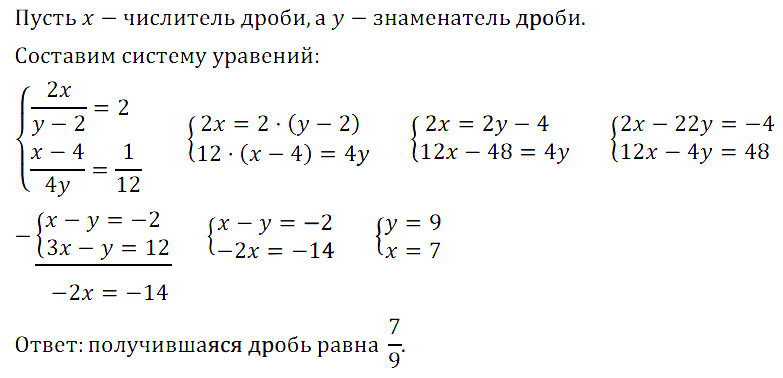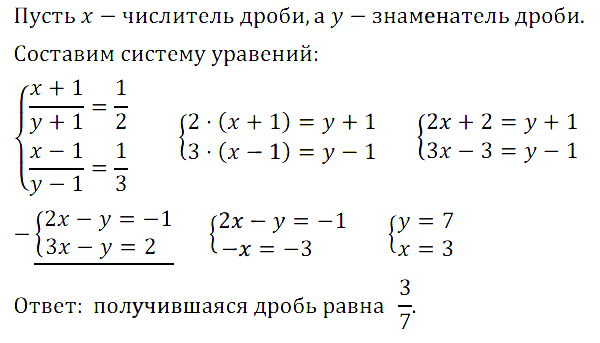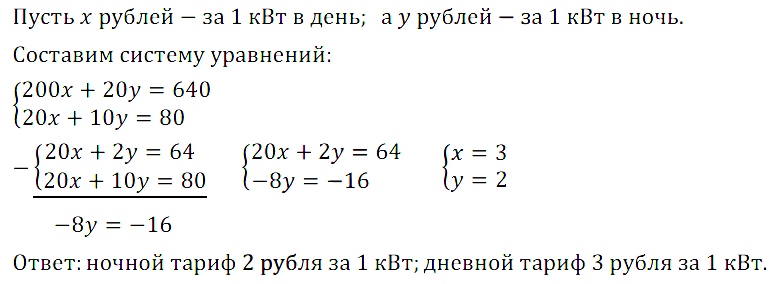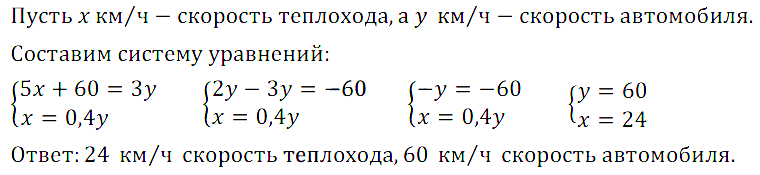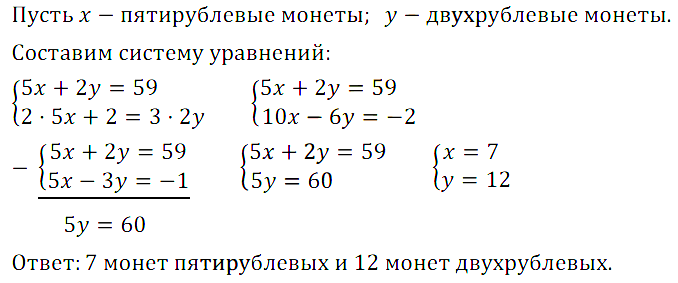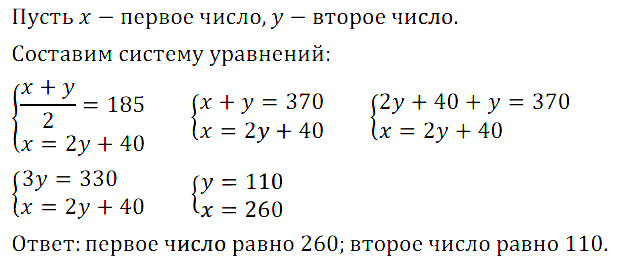Ответы на упражнения 16.1 — 16.38. ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2021). Глава 3. Системы двух линейных уравнений с двумя переменными. § 16. Системы двух линейных уравнений как математические модели реальных ситуации.
Алгебра 7 Мордкович (упр. 16.1 — 16.38)
§ 16. Системы двух линейных уравнений
как математические модели реальных ситуации
Задание № 16.1. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения за 5 ч. Найдите собственную скорость лодки и скорость течения реки.
Задание № 16.2. Два пешехода отправились одновременно навстречу друг другу из пунктов М и N, расстояние между которыми 38 км. Через 4 ч расстояние между ними сократилось до 2 км, а ещё через 3 ч первому пешеходу осталось пройти до пункта N на 7 км меньше, чем второму до М. Найдите скорости пешеходов.
Задание № 16.3. Из пунктов А и В, расстояние между которыми 30 км, навстречу друг другу одновременно вышли два пешехода и встретились через 3 ч 20 мин. Если бы первый вышел на 2 ч раньше второго, то встреча произошла бы через 2,5 ч после выхода второго. Найдите скорости пешеходов.
Задание № 16.4. Катер за 4 ч по течению реки проплывает на 10 км меньше, чем за 6 ч против течения. Найдите собственную скорость катера, если плот по этой реке за 15 ч проплывает такое же расстояние, что и катер за 2 ч по озеру.
Задание № 16.5. Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.
Задание № 16.6. По течению реки лодка за 3 ч 20 мин проходит расстояние 30 км, а против течения за 4 ч — расстояние 28 км. Какое расстояние по озеру пройдёт лодка за 1,5 ч?
Задание № 16.7. Найдите два числа, если известно, что утроенная разность этих чисел на 6 больше их суммы, а удвоенная разность этих чисел на 9 больше их суммы.
Задание № 16.8. Если числитель дроби умножить на 2, а из знаменателя вычесть 2, то получится 2. Если же из числителя вычесть 4, а знаменатель умножить на 4, то получится 1/12. Найдите эту дробь.
Задание № 16.9. Если к числителю и знаменателю дроби прибавить по единице, то получится 1/2, а если из них вычесть по единице, то получится 1/3. Найдите эту дробь.
Задание № 16.10. Два тракториста вспахали вместе 678 га. Первый тракторист работал 8 дней, а второй — 11 дней. Сколько гектаров вспахивал за день каждый тракторист, если первый тракторист за каждые 3 дня вспахивал на 22 га меньше, чем второй за 4 дня?
Задание № 16.11. Две бригады работали на уборке картофеля. В первый день одна бригада работала 2 ч, а вторая — 3 ч, причём ими было собрано 23 ц картофеля. Во второй день первая бригада за 3 ч работы собрала на 2 ц больше, чем вторая за 2 ч. Сколько центнеров картофеля собирала каждая бригада за 1 ч работы?
Задание № 16.12. Зерно перевозили на двух автомашинах различной грузоподъёмности. В первый день было вывезено 27 т зерна, причём одна машина сделала 4 рейса, а другая — 3 рейса. На следующий день вторая машина за 4 рейса перевезла на 11 т зерна больше, чем первая машина за 3 рейса. Сколько тонн зерна перевозили на каждой машине за один рейс?
Задание № 16.13. Для перевозки руды из карьера были отправлены пятитонные и трёхтонные самосвалы. За 1 рейс пятитонные самосвалы перевозят руды на 18 т больше, чем трёхтонные. За рабочий день пятитонные самосвалы совершили 4 рейса, а трёхтонные — 6 рейсов, и всего ими перевезено за день 192 т руды. Сколько самосвалов каждой грузоподъёмности перевозили руду?
Задание № 16.14. На рынке было закуплено 84 кг черешни и вишни, причём черешни куплено на 3 ящика меньше, чем вишни. Сколько ящиков черешни и вишни закуплено по отдельности, если в 1 ящике черешни 8 кг, а вишни 10 кг?
Задание № 16.15. Двое рабочих изготовили 162 детали. Первый работал 8 дней, а второй — 15 дней. Сколько деталей изготовил каждый рабочий, если первый изготовил за 5 дней на 3 детали больше, чем второй за 7 дней?
Задание № 16.16. В квартире Ивана Петровича установлен двухтарифный счётчик, который позволяет учитывать расход электроэнергии по разным тарифам в дневное и ночное время. В январе расход электроэнергии в дневное время составил 200 киловатт–часов (кВт • ч), а в ночное — 20 кВт • ч. По квитанции Иван Петрович заплатил 640 р. В июле расход электроэнергии в дневное время составил 120 кВт • ч, а в ночное — 10 кВт • ч. По квитанции Иван Петрович заплатил 380 р. Вычислите дневной и ночной тариф расхода электроэнергии. (Тариф — это цена 1 киловатт–часа электроэнергии.)
Задание № 16.17. Для учащихся приобрели футбольные и волейбольные мячи, причём волейбольных в 5 раз больше, чем футбольных. На следующий год приобрели новую партию мячей, причём футбольных стало в 6 раз больше, чем было, волейбольных — в 4 раза больше, чем было, а всего мячей стало 52. Сколько мячей закупили в первый год?
Задание № 16.18. Сумма цифр двузначного числа равна 14. Если его цифры поменять местами, то полученное двузначное число будет на 18 меньше первоначального. Найдите исходное число.
Задание № 16.19. Одно число на 140 меньше другого; 60% большего числа на 64 больше 70 % меньшего. Найдите эти числа.
Задание № 16.20. Известно, что 30% числа а на 20 больше, чем 25% числа b, а 30% числа b на 8 больше, чем 20% числа а. Найдите числа а и b.
Задание № 16.21. Среднее арифметическое двух чисел равно 32,5. Найдите эти числа, если известно, что 30% одного из них на 0,25 больше, чем 25% другого.
Задание № 16.22. Полуразность двух чисел равна 14,9. Найдите эти числа, если известно, что 24% первого числа на 0,6 меньше второго.
Задание № 16.23. Путь по морю от города А до города В на 60 км короче, чем по шоссе. Теплоход проходит путь от А до В за 5 ч, а автомобиль — за 3 ч. Найдите скорости теплохода и автомобиля, если известно, что скорость теплохода составляет 40% скорости автомобиля.
Задание № 16.24. Туристы сначала плыли на теплоходе по реке 2 ч, а затем шли 5 ч пешком до конечного пункта. Известно, что по реке они проплыли в 3 раза большее расстояние, чем прошли пешком. Найдите скорости туристов и теплохода, если известно, что скорость теплохода на 26 км/ч больше скорости туристов. Сколько времени понадобилось бы туристам, чтобы пройти весь путь пешком?
Задание № 16.25. На велогонке по гористой местности спортсмен должен был двигаться сначала с горы, потом в гору, а затем в обратном направлении. Путь туда велосипедист преодолел с горы за 20 мин, в гору за 45 мин, а путь обратно — с горы за 25 мин, в гору за 35 мин. Какова скорость велосипедиста в гору и с горы, если путь в одном направлении равен 17 км?
Задание № 16.26. Путь от туристической базы до моря пролегал сначала в гору, а затем с горы. От турбазы до моря туристы шли в гору 45 мин и с горы 40 мин, а обратно — в гору 1 ч 15 мин, а с горы 24 мин. Найдите длину каждого участка пути, если путь в одну сторону равен 6,4 км.
Задание № 16.27. По окружности, длина которой 100 см, движутся равномерно две точки. Они встречаются через каждые 4 с, двигаясь в противоположных направлениях, и через каждые 20 с, двигаясь в одном направлении. Найдите скорости этих точек.
Задание № 16.28. Буратино положил в копилку 59 р. пятирублёвыми и двухрублёвыми монетами. В течение некоторого времени он докладывал туда деньги теми же монетами. Когда Буратино вскрыл копилку, он обнаружил, что пятирублёвых монет стало в 2 раза больше, чем было, а двухрублёвых — в 3 раза больше, чем было, при этом денег пятирублёвыми монетами стало на 2 р. меньше, чем двухрублёвыми. Сколько монет каждого достоинства было в копилке первоначально?
Задание № 16.29. В магазин поступили учебники по физике и математике. Когда продали 50 % учебников по математике и 20 % учебников по физике, что составило в общей сложности 390 книг, учебников по математике осталось в 3 раза больше, чем по физике. Сколько учебников по математике и сколько по физике поступило в магазин?
Задание № 16.30. Среднее арифметическое двух чисел равно 185. Если одно число разделить на другое, то в частном получится 2 и в остатке 40. Найдите эти числа.
Задание № 16.31. Сумма цифр двузначного числа равна 11. Если это число разделить на разность его цифр, то в частном получится 24 и в остатке 2. Найдите исходное число.
Задание № 16.32. Если двузначное число разделить на сумму его цифр, то в частном получится 6 и в остатке 3. Если же разделить его на сумму цифр, увеличенную на 2, то в частном получится 5 и в остатке 5. Найдите исходное число.
Задание № 16.33. Два фрезеровщика, один из которых работал 5 дней, а другой — 8 дней, изготовили 280 деталей. Затем, применив новую фрезу, первый повысил производительность труда на 62,5 %, а второй — на 50 %, и уже за 4 дня совместной работы они изготовили 276 деталей. Сколько деталей изготовили бы они с новой фрезой, если бы, как и раньше, первый работал 5 дней, а второй — 8 дней?
Задание № 16.34. Имеются две отливки стали двух сортов, одна из которых содержит 5 %, а другая — 10 % никеля. Сплавив их вместе, получили отливку, содержащую 8 % никеля. Найдите массу каждой отливки до переплавки, если известно, что вторая отливка содержала никеля на 4 т больше, чем первая.
Задание № 16.35. Имеется лом стали двух сортов с содержанием никеля 5 % и 40 %. Сколько тонн стали каждого сорта нужно взять, чтобы, сплавив их, получить 140 т стали, в которой содержится 30 % никеля?
Задание № 16.36. Купили некоторое количество яблок по 30 р. за 1 кг и некоторое количество груш по 38 р. за 1 кг. Масса яблок и масса груш выражена целыми числами (в кг). Сколько всего купили фруктов, если за покупку заплатили 400 р.?
Задание № 16.37. Из двух пунктов, расстояние между которыми равно 580 км, вышли навстречу друг другу два поезда. До встречи первый был в пути 4 ч, а второй — 3 ч, причём оба двигались с постоянными скоростями и без остановок. Найдите скорости поездов, если известно, что они выражаются целыми числами, кратными 10, и больше 50 км/ч.
Задание № 16.38. Какое двузначное число обладает следующим свойством: если между его цифрами поместить цифру 0, то число увеличится в 6 раз?
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина). Глава 3. Системы двух линейных уравнений с двумя переменными. § 16. Системы двух линейных уравнений как математические модели реальных ситуации (ответы на упражнения 16.1 — 16.38).