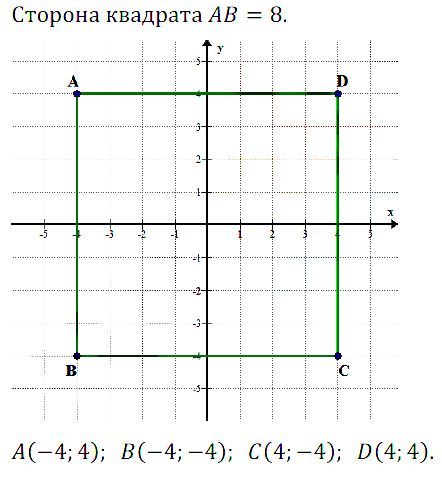ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2021). Глава 2. Линейная функция. § 7. Координатная плоскость (ответы на упражнения 7.1 — 7.40).
§ 7. Часть 1-я ОГЛАВЛЕНИЕ учебника § 7. Часть 2-я
Алгебра 7 Мордкович (упр. 7.1 — 7.40)
§ 7. Координатная плоскость
№ 7.1. Назовите абсциссу и ординату точки: а) М(2; 4); б) N(–3; 6); в) Р(12; –4); г) Q(–3; –0,5).
№ 7.2. Не производя построения, ответьте на вопрос, в каком координатном угле координатной плоскости хОу расположена точка:
а) М(2; 4), N(–3; 6), Р(12; –4), Q(–3; –0,5);
б) Х(–14; –5), Y(–7; 38), K(1; 0), L(0; –4);
в) А(–23; 6), В(13; 16), С(19; –25), D(2; –1/2);
г) R(5/8; –1/7), S(–4/11; –1/12), E(–17/21; 41/43), F(15/31; 1/16).
№ 7.3. Замените символ * каким–либо числом так, чтобы:
а) точка А(5; *) принадлежала первому координатному углу;
б) точка В(*; 3) принадлежала второму координатному углу;
в) точка С(*; –7) принадлежала третьему координатному углу;
г) точка D(12; *) принадлежала четвёртому координатному углу.
Не производя построения, ответьте на вопрос, в каком координатном угле координатной плоскости хОу расположена точка:
№ 7.4. а) А(а; 10), если а > 0; в) С(–с; 5), если с > 0;
б) В(17; b), если b < 0; г) D(–8; d), если d < 0.
№ 7.5. а) Р(х; у), если х > 0, у > 0; б) Q(x; у), если х > 0, у < 0; в) R(x; у), если х < 0, у > 0; г) S(x; у), если х < 0, у < 0.
№ 7.6. В каком координатном угле координатной плоскости расположена данная точка:
а) М(а; b), если а < 0, b < 0; б) N(–a; –b), если а > 0, b < 0; в) К(а; –b), если а < 0, b > 0; г) L(–а; b), если а > 0, b > 0?
№ 7.7. Найдите координаты точек, изображённых на рис. 2: а) А, С, М, S; б) R, D, К, Q; в) Р, Y, В, F; г) Е, N, X, Z.
Какой признак объединяет каждую группу точек?
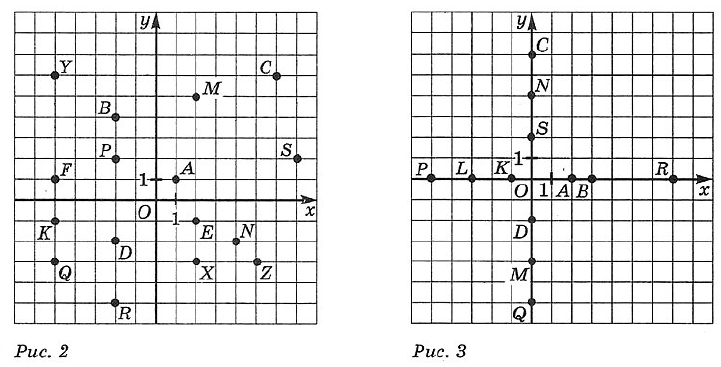
№ 7.8. Найдите координаты точек, изображённых на рис. 3: а) А, В, К, Р, L, R; б) С, D, М, N, Q, S.
Какой общий графический признак объединяет эти точки? Как этот общий признак выражается при записи координат точек? Где расположены все точки, у которых абсцисса равна нулю; ордината равна нулю? Составьте аналитическую модель множества точек, лежащих на оси х; на оси у.
№ 7.9. Найдите координаты точек, изображённых на рис. 4.
Что общего в записи координат каждой группы точек? Как расположены на координатной плоскости все точки, имеющие одинаковую абсциссу? Составьте аналитическую модель прямой, параллельной оси у.
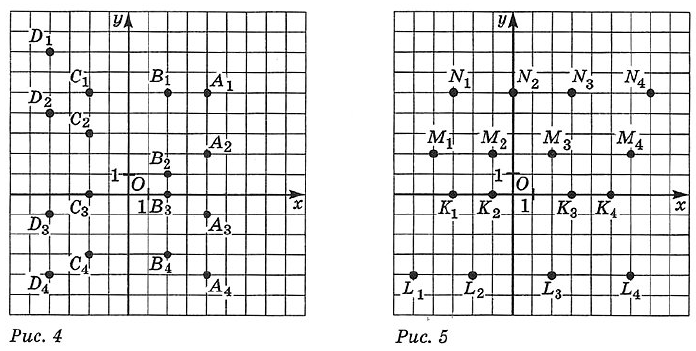
№ 7.10. Найдите координаты точек, изображённых на рис. 5.
Что общего в записи координат каждой группы точек? Как расположены на координатной плоскости все точки, имеющие одинаковую ординату? Составьте аналитическую модель прямой, параллельной оси х.
Прочитайте п. 2 в § 7 учебника до примера 2 (стр. 39)
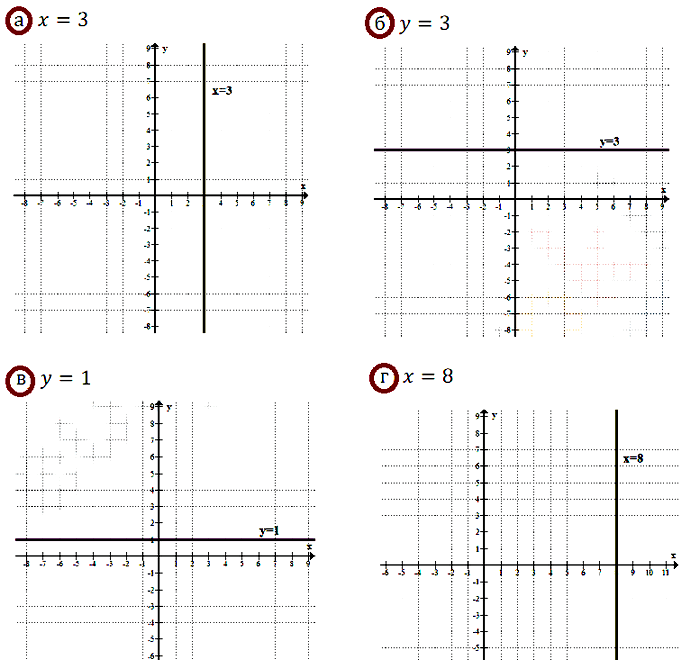
№ 7.11. Постройте прямую, удовлетворяющую уравнению:
7.11 а) х = 3; б) у = 3; в) у = 1; г) х = 8.
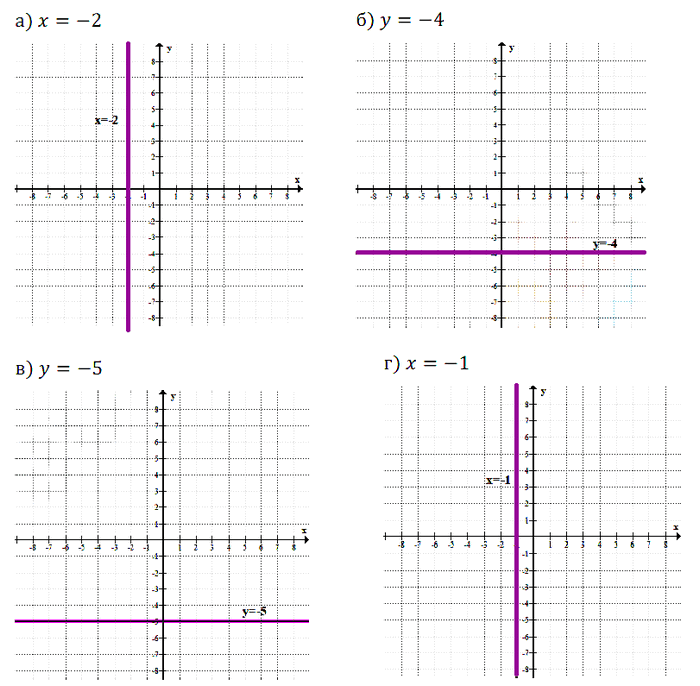
№ 7.12. а) х = –2; б) у = –4; в) у = –5; г) х = –1.
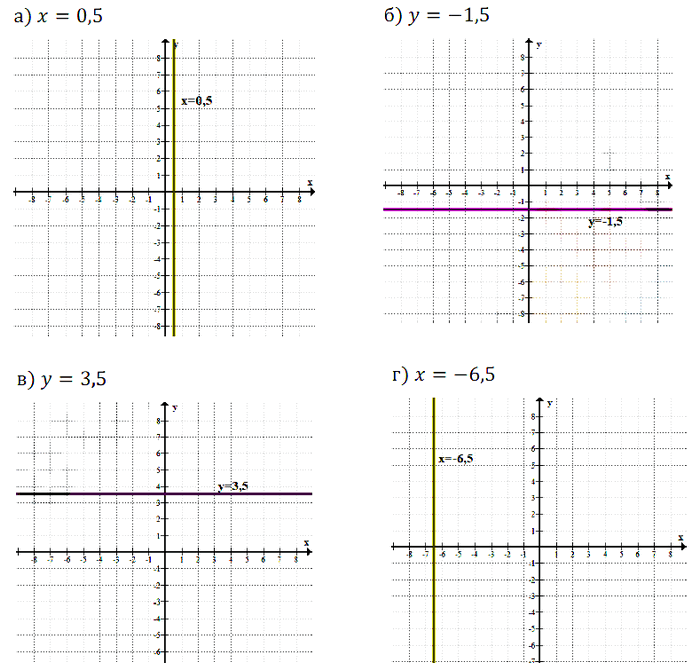
№ 7.13. а) х = 0,5; б) у = –1,5; в) у = 3,5; г) х = –6,5.
№ 7.14. Какая прямая удовлетворяет уравнению: а) х = 0; б) у = 0?
№ 7.15. Как расположены в координатной плоскости все точки, имеющие абсциссу, равную: а) 5; б) –7; в) 9; г) –1?
№ 7.16. Как расположены в координатной плоскости все точки, имеющие ординату, равную: а) –3; б) 8; в) –12; г) 4?
В координатной плоскости хОу постройте прямую, удовлетворяющую уравнению:
№ 7.17. а) 2х = 4; б) –х + 4 = 0; в) –3х = 9; г) 2х – 6 = 0.
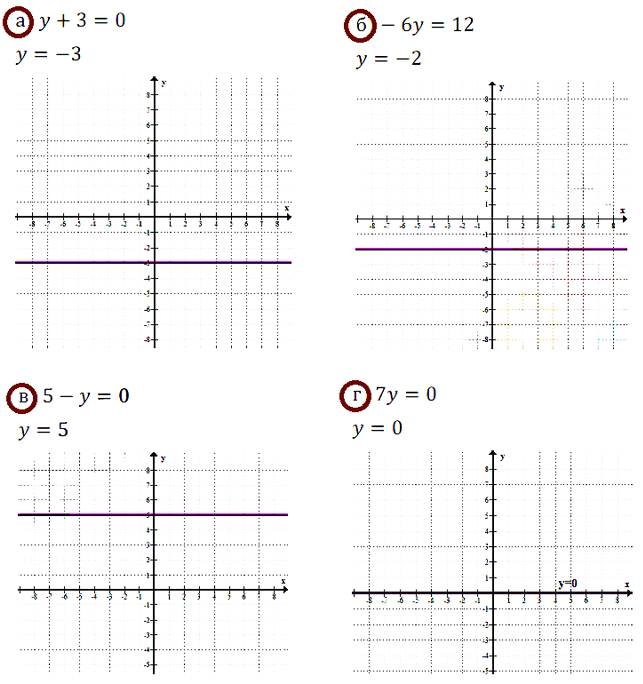
№ 7.18. а) у + 3 = 0; б) –6у = 12; в) 5 – у = 0; г) 7у = 0.
Разберите в учебнике решение примера 2 из § 7.
№ 7.19. На координатной плоскости хОу найдите точку, симметричную данной точке относительно начала координат:
а) А(5; 7); б) В(0; 8); в) С(7; –1); г) D(–3; 0).
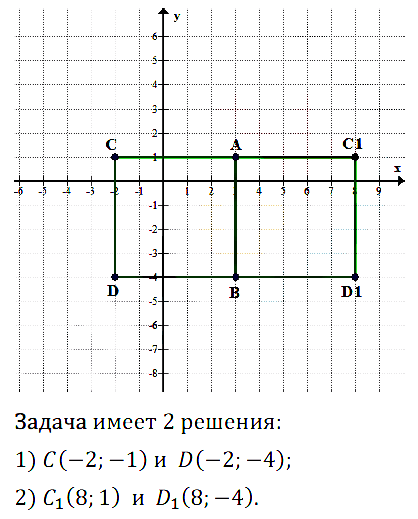
№ 7.33. Найдите координаты вершин С и В квадрата ABCD, если известны координаты вершин А(3; 1) и В(3; –4). Сколько решений имеет задача?
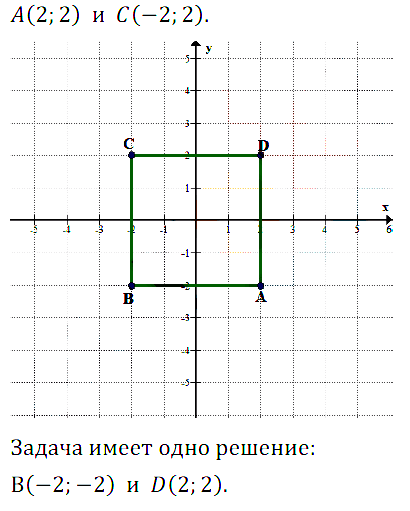
№ 7.34. Известны координаты двух противоположных вершин квадрата ABCD: А(2; –2) и С(–2; 2). Найдите координаты двух других вершин. Сколько решений имеет задача?
№ 7.35. Длина стороны квадрата ABCD равна 6, а координаты вершины А равны (–2; 3). Найдите координаты остальных вершин, зная, что сторона АВ квадрата параллельна оси ординат и что начало координат лежит внутри квадрата.
№ 7.36. Квадрат со стороной 8 расположен так, что центр его находится в начале координат, а стороны параллельны осям координат. Определите координаты вершин квадрата.
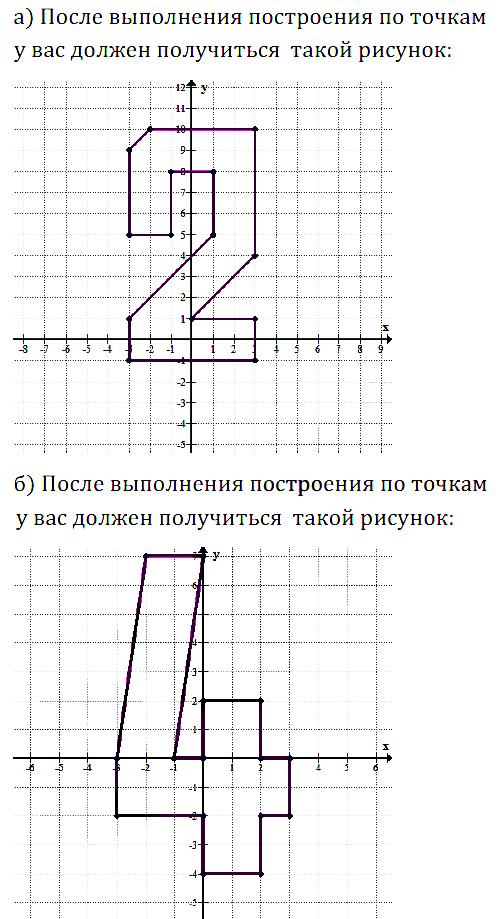
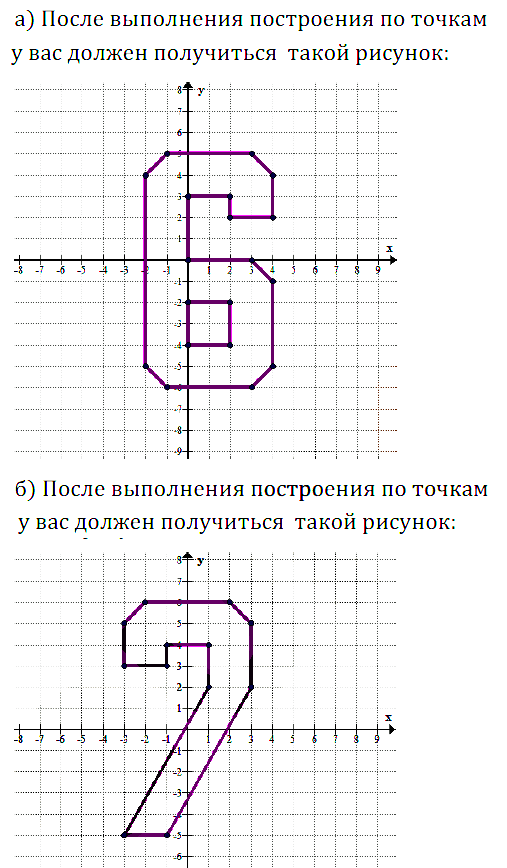
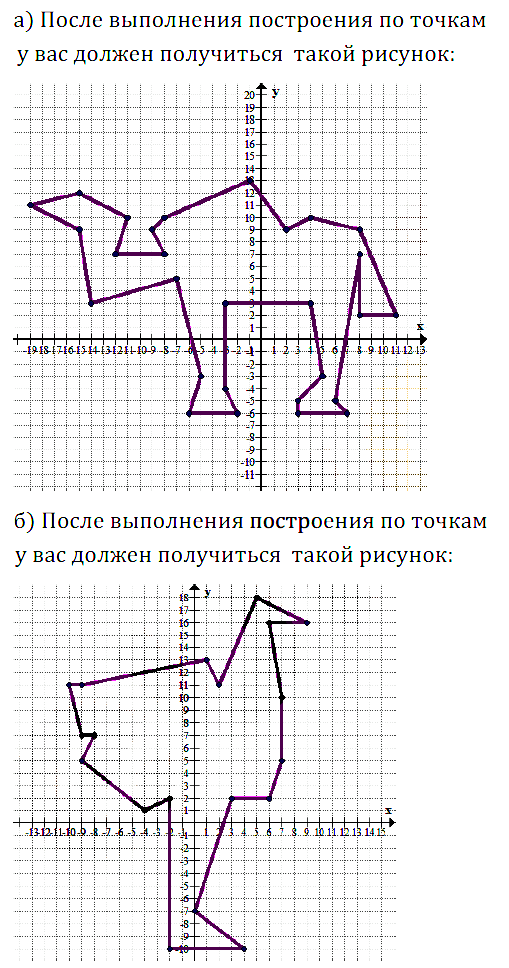
На координатной плоскости постройте точки по заданным координатам и последовательно соедините их отрезками. Какая фигура при этом получится?
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2021). Глава 2. Линейная функция. § 7. Координатная плоскость (ответы на упражнения 7.1 — 7.40).

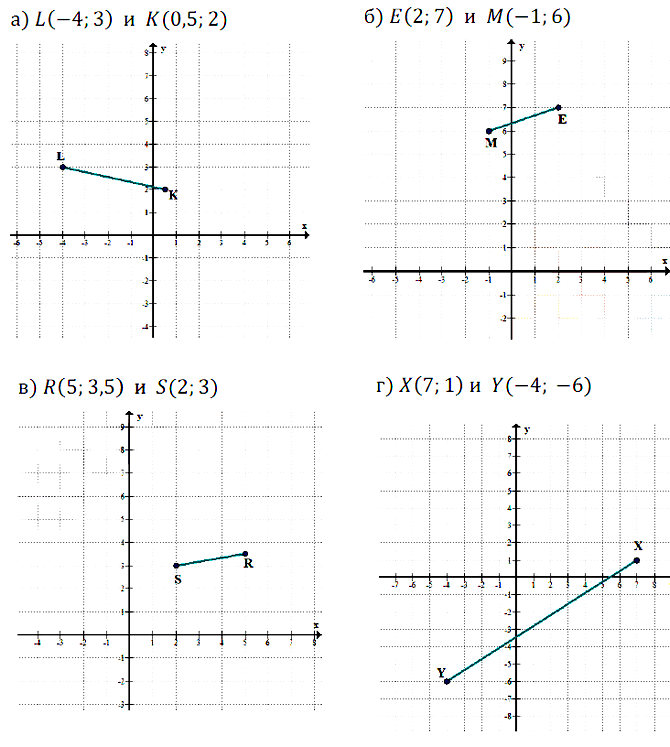
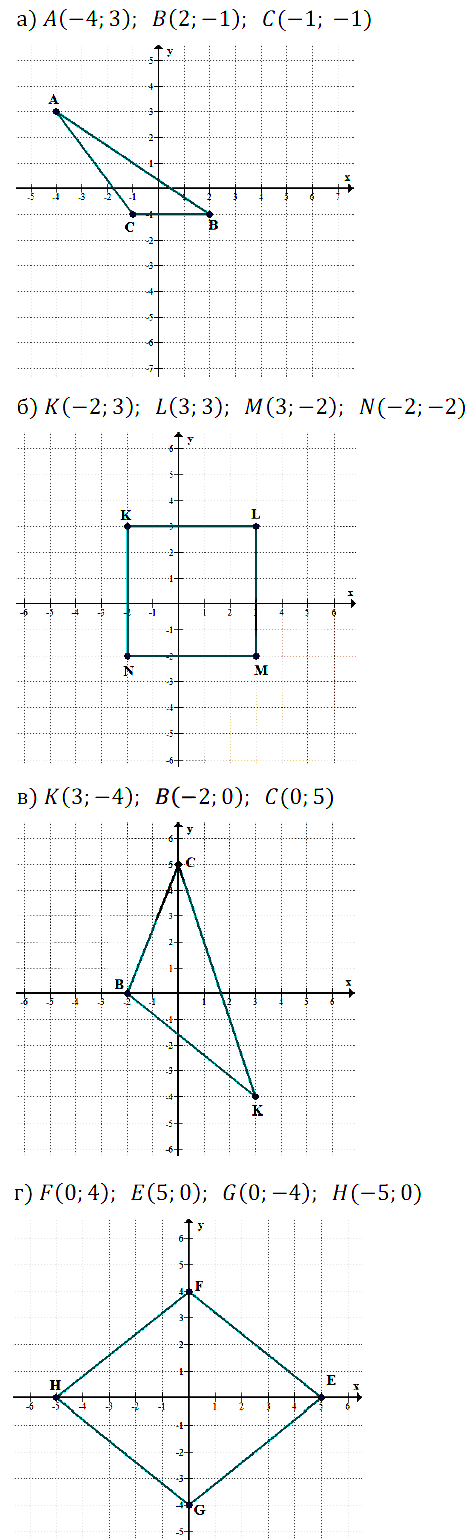
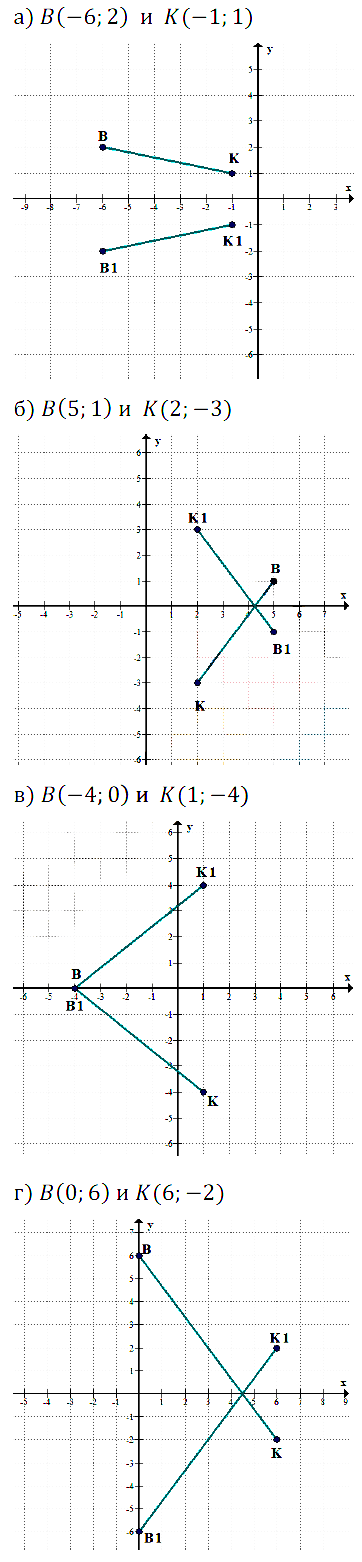
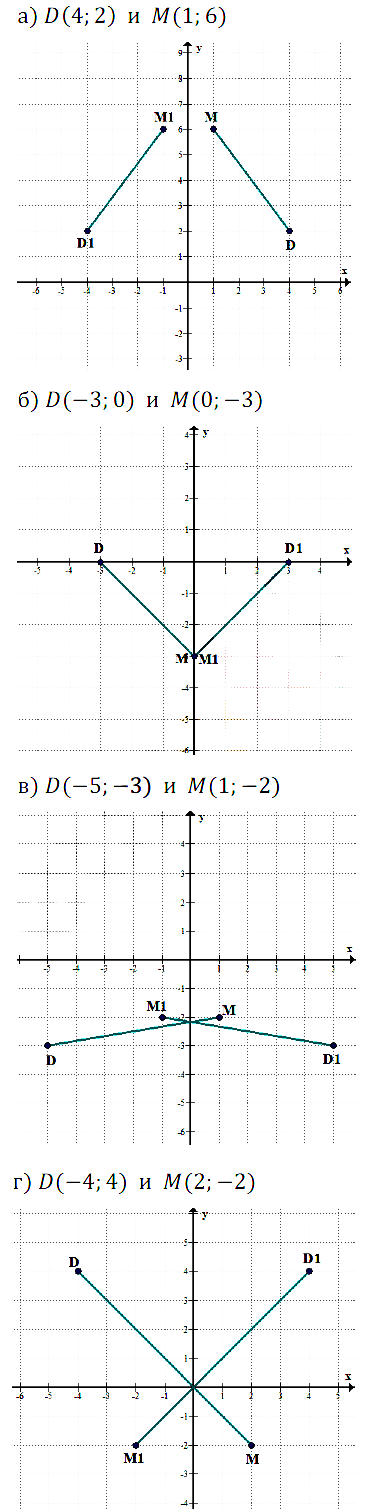
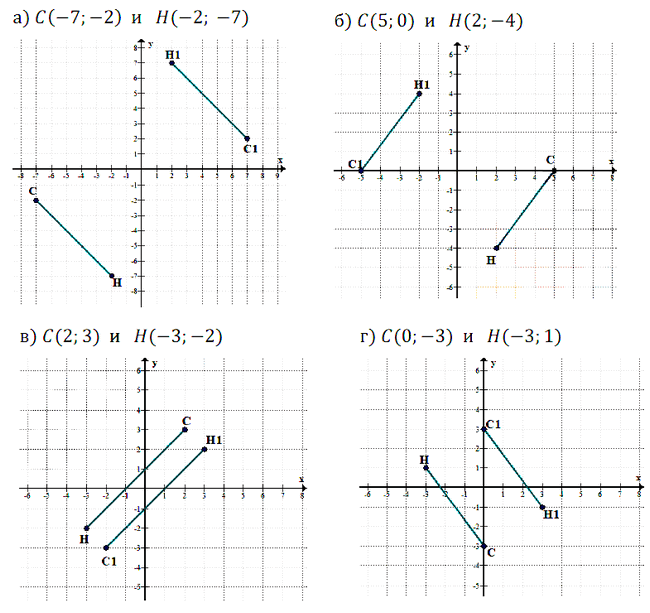
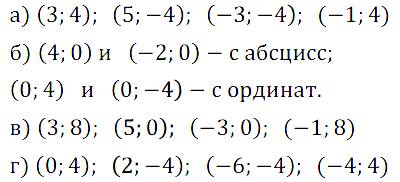
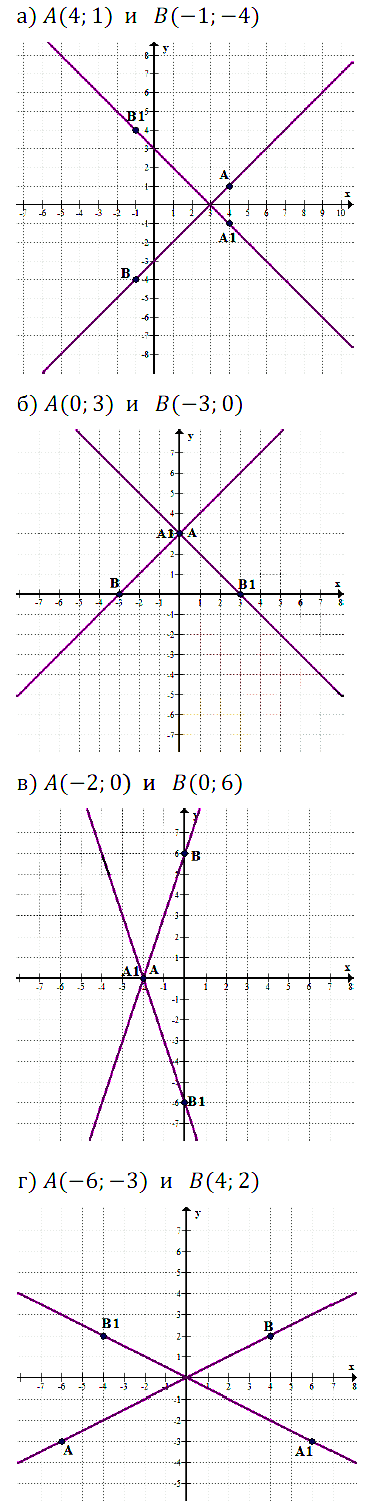
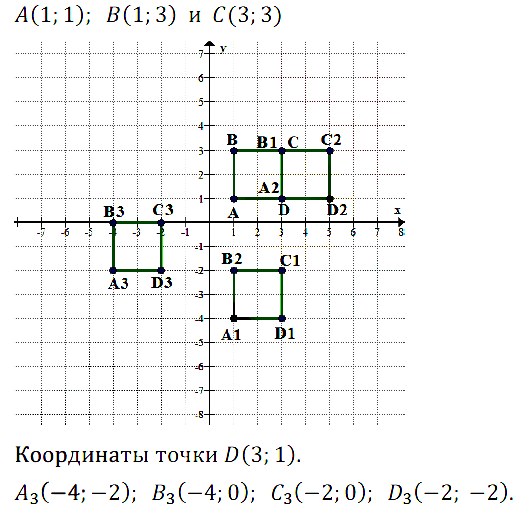
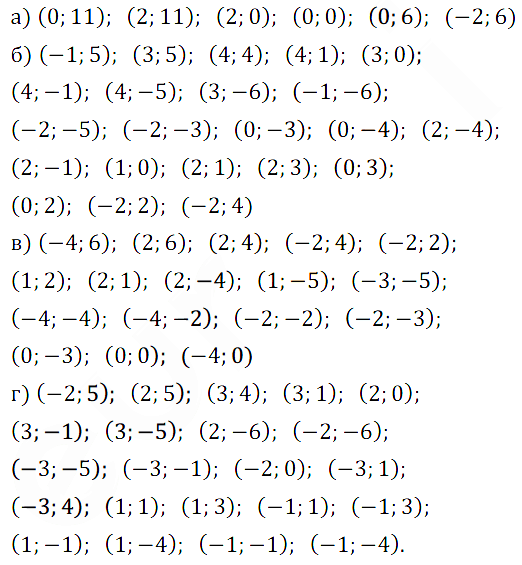
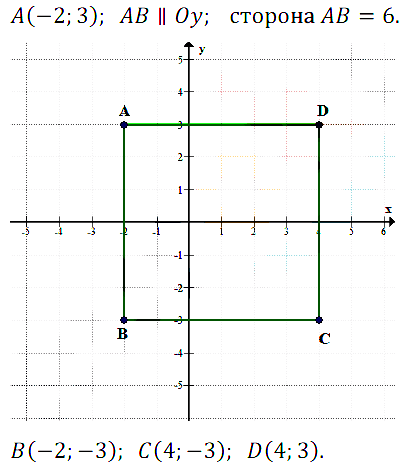 Из того, что АВ параллельна оси координат следует, что абсцисса точки В равна абсциссе точки А. Из того, что начало координат лежит внутри квадрата и ордината точки А положительна, следует, что В(–2, 3 – 6), т.е. В(–2, –3); С(–2 + 6, –3) => С(4, –3); D(–2 + 6, 3) => D(4, 3).
Из того, что АВ параллельна оси координат следует, что абсцисса точки В равна абсциссе точки А. Из того, что начало координат лежит внутри квадрата и ордината точки А положительна, следует, что В(–2, 3 – 6), т.е. В(–2, –3); С(–2 + 6, –3) => С(4, –3); D(–2 + 6, 3) => D(4, 3).