7 класс Онлайн

Геометрия ГДЗ Атанасян Учебник. Задания 156 — 185. Решебник практических заданий и задач из учебника «Геометрия 7 класс» УМК Атанасян, Бутузов и др. Глава II Треугольники. Дополнительные задачи. Ответы на практические задания и задачи представлены для родителей в конце статьи.

Геометрия (Атанасян) Учебник

Дополнительные задачи

156. □ Периметр треугольника АВС равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона АВ меньше стороны АС на 1 см. Найдите стороны треугольника.
157. □ В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковых сторон на 3 см. Найдите стороны треугольника.
158. Основание равнобедренного треугольника равно 8 см. Медиана, проведённая к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2 см больше периметра другого. Найдите боковую сторону данного треугольника.
159. Докажите, что два равнобедренных треугольника равны, если боковая сторона и угол, противолежащий основанию, одного треугольника соответственно равны боковой стороне и углу, противолежащему основанию, другого треугольника.
160. Прямая а проходит через середину отрезка АВ и перпендикулярна к нему. Докажите, что: а) каждая точка прямой а равноудалена от точек А и В; б) каждая точка, равноудалённая от точек А и В, лежит на прямой а.
161. В треугольниках АВС и А₁В₁С₁ медианы AM и А₁М₁ равны, ВС = В₁С₁ и ∠AMB = ∠A₁M₁B₁. Докажите, что ΔАВС = ΔА₁В₁С₁.
162. На рисунке 92 треугольник ADE равнобедренный, DE — основание. Докажите, что:
     а) если BD = СЕ, то ∠CAD = ∠BAE и АВ = АС; б) если ∠CAD = ∠BAE, то BD = CE и АВ = АС.
163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедренного треугольника.
164. На сторонах равностороннего треугольника АВС отложены равные отрезки AD, BE и CF, как показано на рисунке 93. Точки D, Е, F соединены отрезками. Докажите, что треугольник DEF — равносторонний.

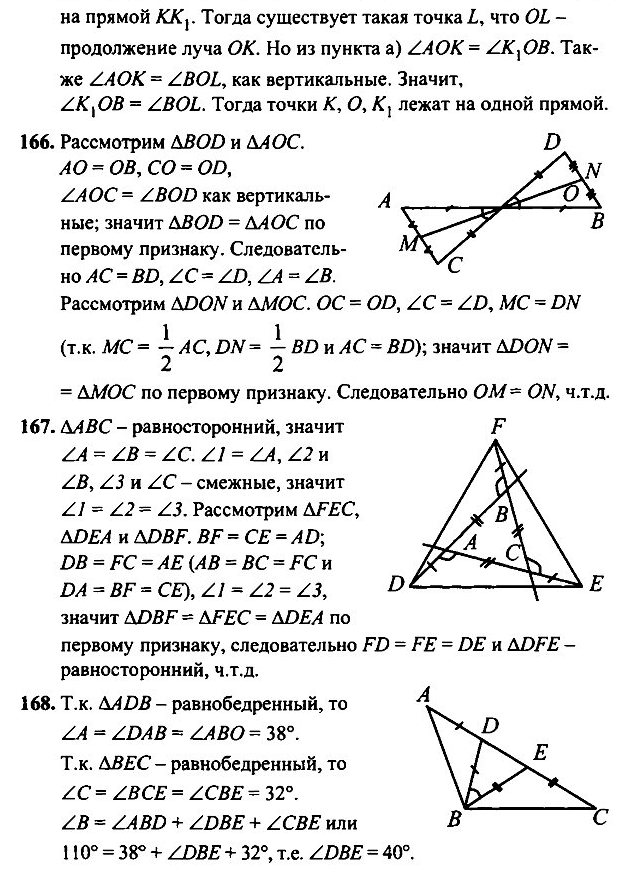
165. Отрезки АВ и CD пересекаются в их общей середине О. На отрезках АС и BD отмечены точки К и К₁ так, что АК = ВК₁. Докажите, что: а) ОК = ОК₁; б) точка О лежит на прямой КК₁.
166. Отрезки АВ и CD пересекаются в их общей середине О. Точки М и N — середины отрезков АС и BD. Докажите, что точка О — середина отрезка MN.
167. Стороны равностороннего треугольника АВС продолжены, как показано на рисунке 94, на равные отрезки AD, СЕ, BF. Докажите, что треугольник DEF — равносторонний.
168. В треугольнике ABC ∠A = 38°, ∠B = 110°, ∠C = 32°. На стороне АС отмечены точки D и Е так, что точка D лежит на отрезке АЕ, BD = DA, ВЕ = ЕС. Найдите угол DBE.
169. На рисунке 95 OC = OD, ОВ = ОЕ. Докажите, что AB = EF. Объясните способ измерения ширины озера (отрезка АВ на рисунке 95), основанный на этой задаче.
170. Докажите, что треугольники АВС и А₁В₁С₁ равны, если АВ = А₁В₁, ∠A = ∠A₁, AD = A₁D₁, где AD и A₁D₁ — биссектрисы треугольников.
171. В треугольниках АВС и ADC стороны ВС и AD равны и пересекаются в точке О, ∠OAC = ∠OCA. Докажите, что треугольники АВО и СDO равны.
172. На рисунке 96 AC = AD, AB ⊥ CD. Докажите, что BC = BD и ∠ACB = ∠ADB.
173. * Докажите, что угол, смежный с углом треугольника, больше каждого из двух других углов треугольника.
174. * Докажите, что ΔАВС = ΔА₁В₁С₁, если ∠A = ∠A₁, ∠B = ∠B₁, ВС = В₁С₁.
175. * На сторонах угла XOY отмечены точки А, В, С и D так, что ОА = ОВ, AC = BD (рис. 97). Прямые AD и ВС пересекаются в точке Е. Докажите, что луч ОЕ — биссектриса угла XOY. Опишите способ построения биссектрисы угла, основанный на этом факте.
176. * Докажите, что треугольники АВС и А₁В₁С₁ равны, если АВ = А₁В₁, АС = А₁С₁, AM = А₁М₁, где AM и А₁М₁ — медианы треугольников.
177. * Даны два треугольника: АВС и А₁В₁С₁. Известно, что АВ = А₁В₁, АС = А₁С₁, ∠A = ∠AX. На сторонах АС и ВС треугольника АВС взяты соответственно точки К и L, а на сторонах А₁С₁ и В₁С₁ треугольника А₁В₁С₁ — точки К₁ и L₁ так, что АК = А₁К₁, LC = L₁C₁. Докажите, что: a) KL = K₁L₁, б) AL = A₁L₁.
178. * Даны три точки А, В, С, лежащие на одной прямой, и точка D, не лежащая на этой прямой. Докажите, что по крайней мере два из трёх отрезков AD, BD и CD не равны друг другу.
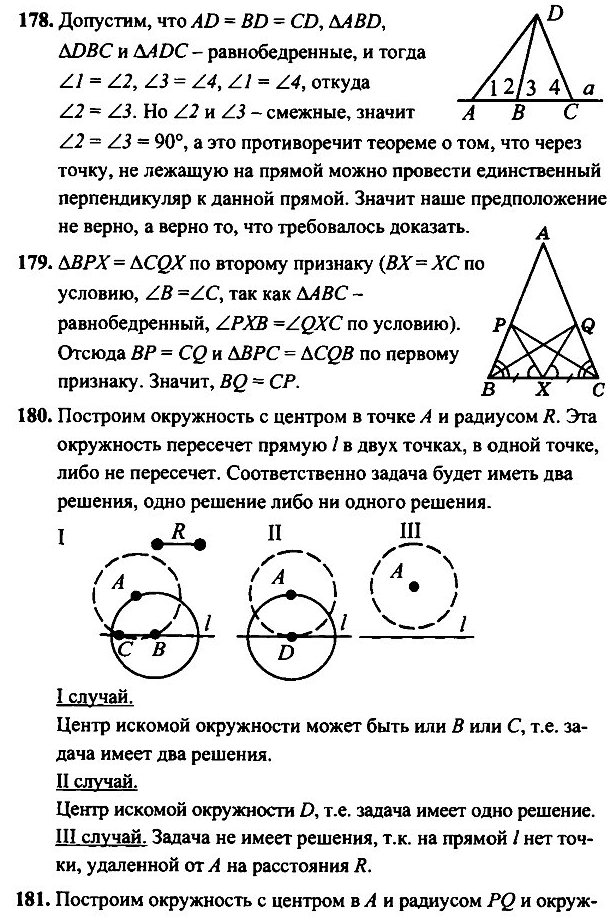
179. * На боковых сторонах АВ и АС равнобедренного треугольника АВС отмечены точки Р и Q так, что ∠PXB = ∠QXC, где X — середина основания ВС. Докажите, что BQ = CP.
180. Постройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой.
181. Постройте окружность данного радиуса, проходящую через две данные точки.
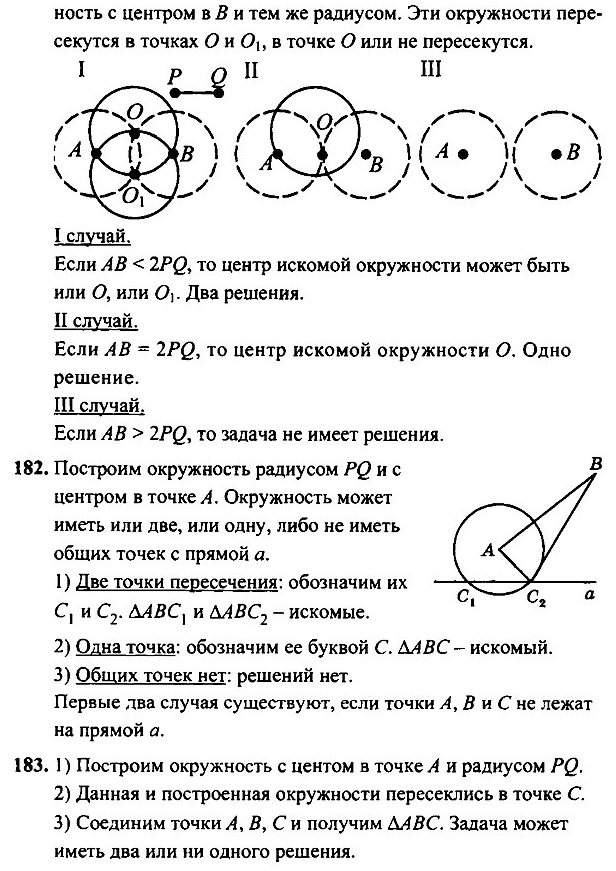
182. Даны прямая а, точки А, В и отрезок PQ. Постройте треугольник АВС так, чтобы вершина С лежала на прямой а и AC = PQ.
183. Даны окружность, точки А, В и отрезок PQ. Постройте треугольник АВС так, чтобы вершина С лежала на данной окружности и AC = PQ.
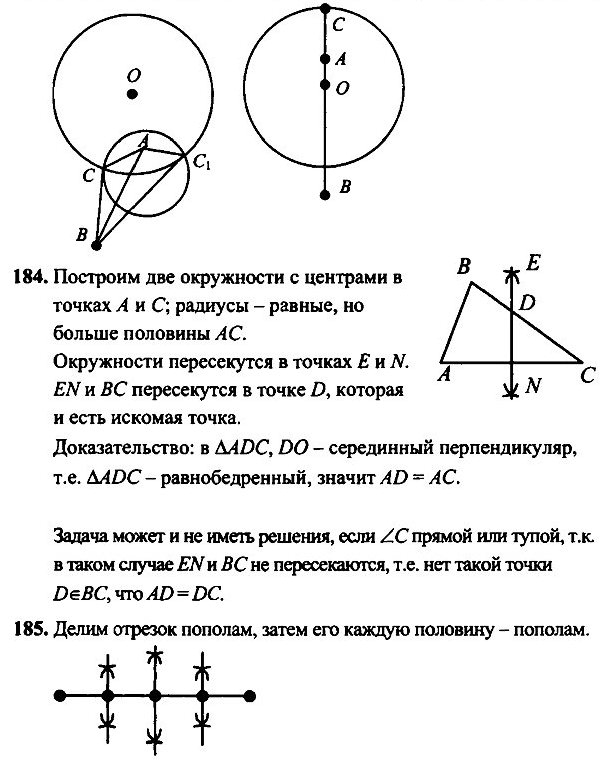
184. На стороне ВС треугольника АВС постройте точку, равноудалённую от вершин А и С.
185. С помощью циркуля и линейки разделите данный отрезок на четыре равные части.

ОТВЕТЫ на задания 156 — 185:

Вы смотрели: ГДЗ Атанасян Учебник. Задания 156 — 185. Решебник практических заданий и задач из учебника «Геометрия 7 класс» УМК Атанасян, Бутузов и др. Глава II Треугольники. Дополнительные задачи. Ответы.

Вернуться к Списку заданий учебника по Геометрии 7 класс Атанасян.