ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович (2019). Глава 6. Многочлены. Арифметические операции над многочленами. § 35. Процентные частоты. ОТВЕТЫ на упражнения 35.1 — 35.8). Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 Мордкович (упр. 35.1 — 35.8)
§ 35. Процентные частоты
Результаты некоторого измерения распределены следующим образом:
| Результат | –3 | –1 | 2 | 4 | 7 |
| Сколько раз встретился | 2 | 6 | 4 | 3 | 2 |
№ 35.1. а) Найдите объём и размах измерения.
б) Найдите моду измерения. Сколько раз она встретилась в измерении?
в) Найдите частоту моды и представьте её в виде обыкновенной дроби.
г) Представьте частоту моды в виде десятичной дроби; в процентах.
№ 35.2. а) Найдите частоту результата 7. Представьте её в виде обыкновенной дроби; в виде десятичной дроби; в процентах.
б) Найдите процентную частоту остальных результатов.
в) Заполните таблицу распределения процентных частот:
| Результат | –3 | –1 | 2 | 4 | 7 |
| Частота, % |
г) Перечислите те результаты, каждый из которых составляет менее 20 % общего числа результатов.
По итогам чемпионата Европы по футболу 2008 года на одном из футбольных сайтов определялся лучший игрок сборной России. Проголосовало 7000 человек. Результаты голосования занесены в таблицу:
| Игрок | Кол–во голосов «за», % | Игрок | Кол–во голосов «за», % |
| Анюков | 3,8 | Колодин | 8,4 |
| Аршавин | 31,8 | Павлюченко | |
| Жирков | Семак | 6,6 | |
| Зырянов | 4,9 | Семшов | 1,3 |
№ 35.3. а) Сколько человек составили 0,1 % от числа проголосовавших?
б) Каков (в процентах) результат голосования за игроков «Зенита», на тот момент состоявших в команде (Анюкова, Аршавина, Зырянова)?
в) Результаты голосования за Жиркова и Павлюченко оказались одинаковыми. Чему (в процентах) они равны?
г) Сколько человек проголосовало за Жиркова и Павлюченко вместе?
№ 35.4. а) Сколько человек проголосовало за Аршавина?
б) Сколько человек проголосовало за трёх лучших по итогам опроса игроков?
в) На сколько человек больше проголосовали за нападающих (Аршавина, Павлюченко), чем за защитников (Анюкова, Жиркова, Колодина)?
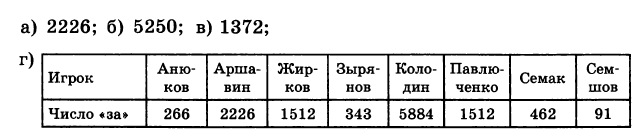
г) Заполните таблицу распределения числа голосовавших:
| Игрок | Кол–во голосов «за» | Игрок | Кол–во голосов «за» |
| Анюков | Колодин | ||
| Аршавин | Павлюченко | ||
| Жирков | Семак | ||
| Зырянов | Семшов |
Приведите к стандартному виду многочлены:
1) х2 + 2у3(1 + 3ху); 2) (8а3 + b)(1 + 0,5а)а3;
3) b(d2 – 3)2(d2 + 1); 4) (а – 12b4)(а – 0,5b4);
5) 24х(х2 + 2)(2 + 0,25x2); 6) (8х2у + z)(t – 0,125z2);
7) (1 – 3с)(1 + с)(1 – 2с).
В каждом многочлене подчеркните одночлен наибольшей степени.
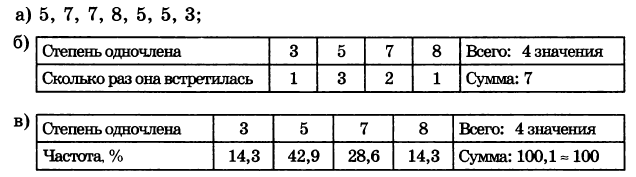
№ 35.5. а) Запишите поочерёдно значения степеней подчёркнутых одночленов.
б) Составьте таблицу распределения степеней, найденных в пункте а).
в) Составьте таблицу распределения процентных частот.
1) 6ху4 + 2у3 + х2;
2) 8а6 + а3b + 4a7 + 0,5a4b;
3) bd6 – 5bd4 + 3bd2 + 9b;
4) –12,5ab4 + a2 + 6b8;
5) 60x3 + 96x + 6x5;
6) 8tx2y + tz – x2yz2 – 0,125z3
7) 6c3 + c2 – 4c + 1.
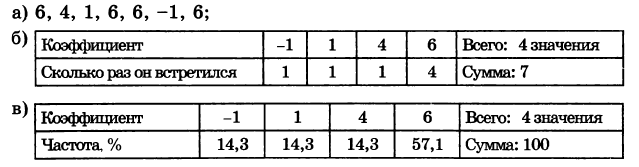
№ 35.6. а) Запишите поочерёдно коэффициенты подчёркнутых одночленов.
б) Составьте таблицу распределения коэффициентов, найденных в пункте а).
в) Составьте таблицу распределения процентных частот. Постройте круговую диаграмму распределения процентных частот.
г) Первый многочлен произвольно выбирают из многочленов 2а + 1 или а2 – 2а. Второй многочлен произвольно выбирают из многочленов 2а – а2, 3 – 2а или 1 – а2.
№ 35.7. Найдите вероятность того, что степень суммы выбранных многочленов:
а) меньше 3; б) больше 2; в) равна 2; г) равна нулю.
№ 35.8. Найдите вероятность того, что степень произведения выбранных многочленов:
а) меньше 5; б) меньше 1; в) равна 3; г) равна 4.
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 6. Многочлены. Арифметические операции над многочленами. ОТВЕТЫ на упражнения 35.1 — 35.8.