ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович (2019). Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 36. Что такое разложение многочленов на множители и зачем оно нужно. ОТВЕТЫ на упражнения 36.1 — 36.18). Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 Мордкович (упр. 36.1 — 36.18)
§ 36. Что такое разложение многочленов на множители и зачем оно нужно
Нажмите на спойлер, чтобы посмотреть ответ на задание:
Решите уравнение:
Задание № 36.1. а) х(х + 2) = 0; б) (х + 1)(х + 4) = 0; в) z(z – 1,6) = 0; г) (у + 2)(у – 6) = 0.
Задание № 36.2. а) m(m + 1 )(m + 2) = 0; б) n2(n – 3)(n – 8) = 0; в) р(р + 13)(р – 17) = 0; г) q3(q – 21)(q – 105) = 0.
Задание № 36.3. а) (2х + 3)(3х – 6) = 0;
б) (9у + 18)(12у – 4)(36y – 72) = 0;
в) (4а – 8)(6а – 10) = 0;
г) (4t – 1)(8t – 3)(12t – 17) = 0.
Задание № 36.4. Представьте многочлен р(х) в виде произведения многочлена и одночлена, если:
а) р(х) = 2х2 + х; б) р(х) = 6x3 – 3х2 + Зх; в) р(х) = 3x3 – 12x; г) р(х) = 5х4 + 5x3 – 10х2.
Задание № 36.5. Представьте многочлен р(х) в виде произведения многочлена и одночлена и найдите, при каких значениях х выполняется равенство р(х) = 0, если: а) р(х) = 5х2 – 10x; б) р(х) = х2 + 6x3; в) р(х) = 7х2 + 21х; г) р(х) = 4х4 – x3.
Задание № 36.6. Решите уравнение:
а) х2 – x = 0; б) 2х2 + 4х = 0; в) 3х2 – 7х = 0; г) х2 = 4х.
Задание № 36.7. Воспользовавшись формулой а2 – b2 = (а – b)(а + b), представьте многочлен р(х) в виде произведения двух многочленов, если:
а) р(х) = х2 – 4; б) р(х) = 9 – 4х2; в) р(х) = х2 – 9; г) р(х) = 4 – 9х2.
Задание № 36.8. Разложите многочлен р(х) на множители и найдите, при каких значениях х выполняется равенство р(х) = 0, если:
а) р(х) = х2; б) р(х) = х2 – 0,64; в) р(х) = х2 – 49; г) р(х) = х2 – 25/36.
Задание № 36.9. Решите уравнение:
а) х2 – 16 = 0; б) у2 – 25 = 0; в) z2 – 36 = 0; г) t2 – 100 = 0.
Вычислите наиболее рациональным способом:
Задание № 36.10. а) 1,8 • 0,6 + 1,8 • 0,4; б) 1,52 – 1,5 • 11,5; в) 3,6 • 1,3 – 0,3 • 3,6; г) 1,3 • 8,7 + 1,32.
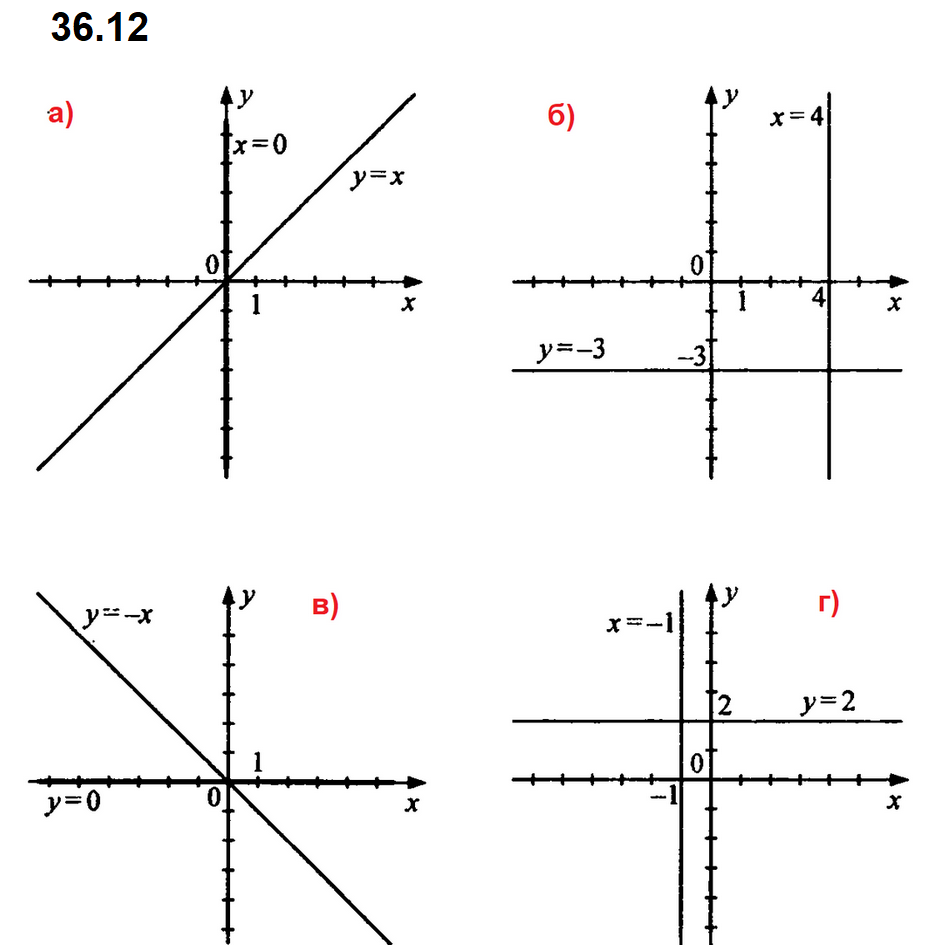
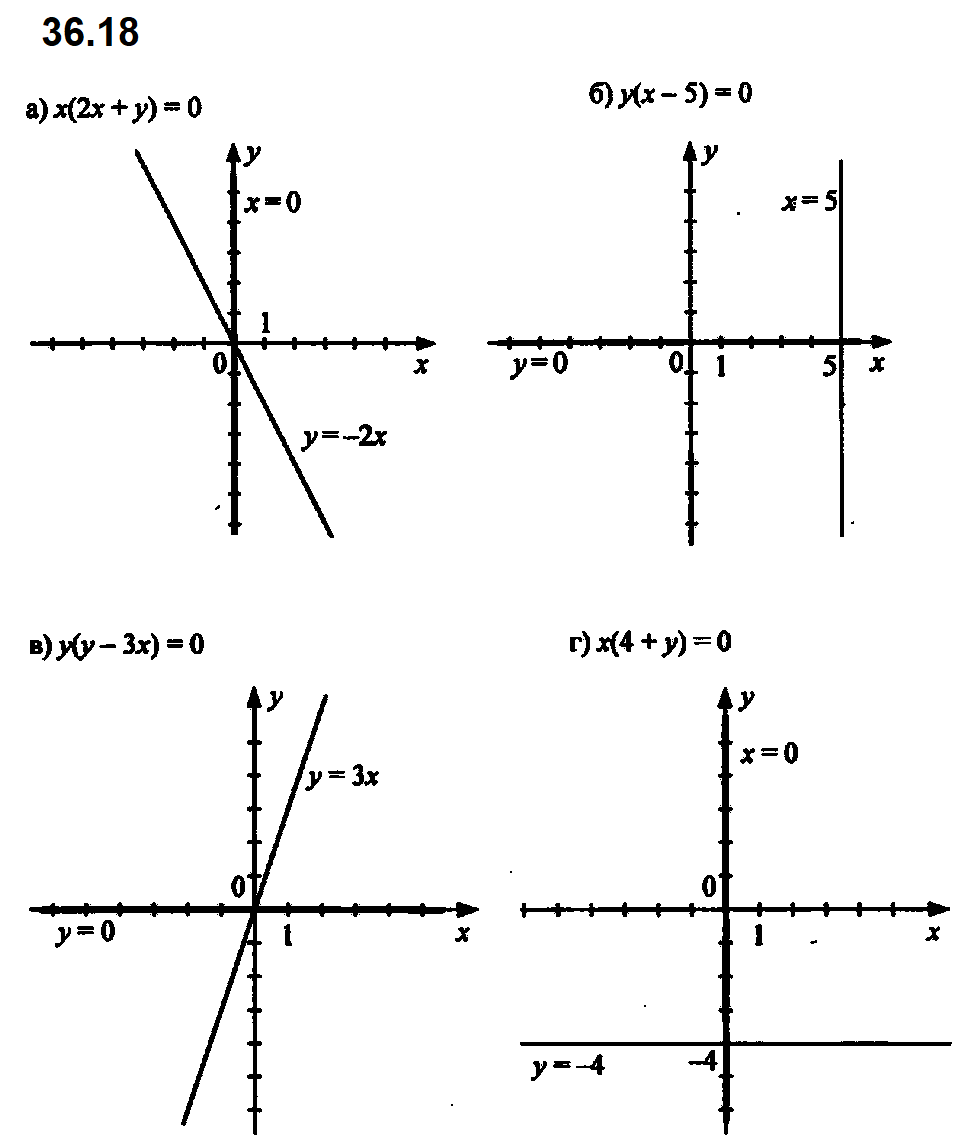
№ 36.18. Постройте график уравнения: а) 2x^2 + ху = 0; б) ху — 5у = 0; в) у^2 — 3ху = 0; г) 4х + ху = 0.
№ 36.19. Докажите, что: а) (41^2 + 41 • 59) ︙ 100; б) (95^2 — 71^2) ︙ 12; б) (111^2 — 111 • 67) ︙ 11; г) (111^2 — 39^2) ︙ 40.
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 7. Разложение многочленов на множители. ОТВЕТЫ на упражнения 36.1 — 36.18.
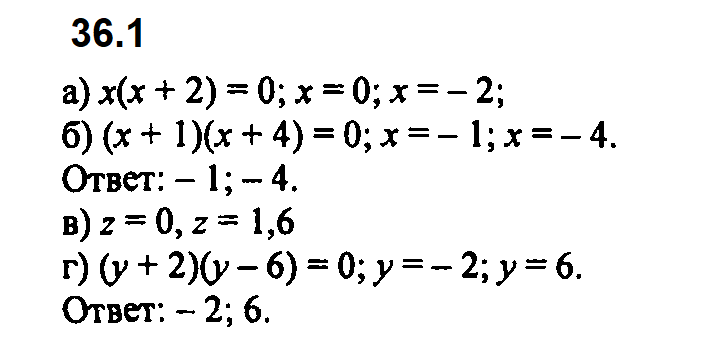
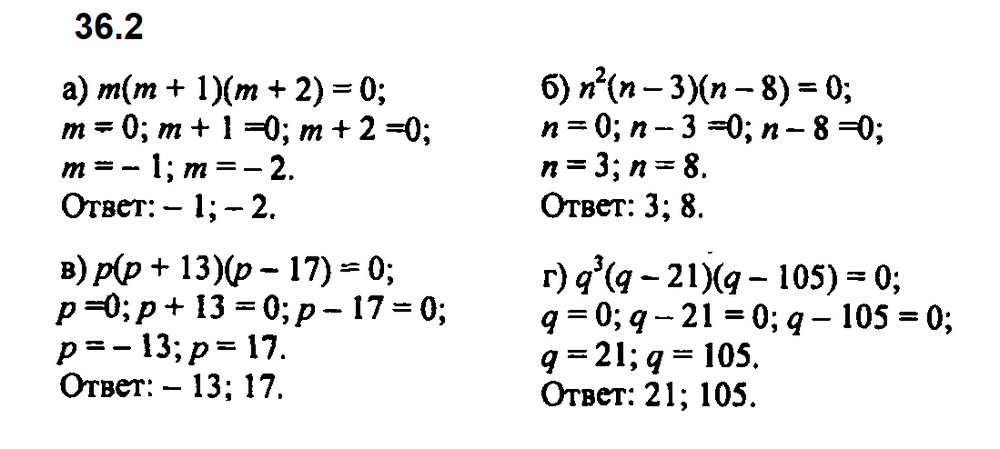
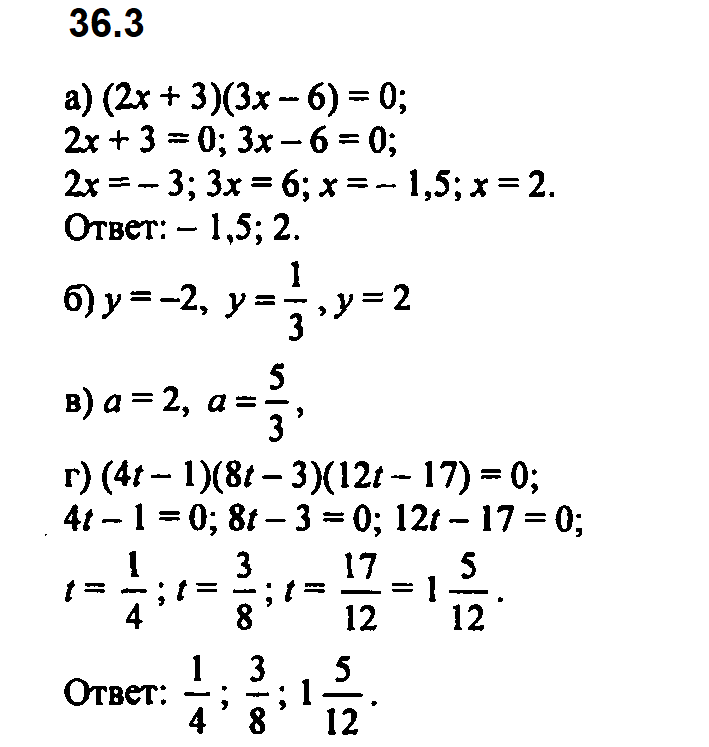
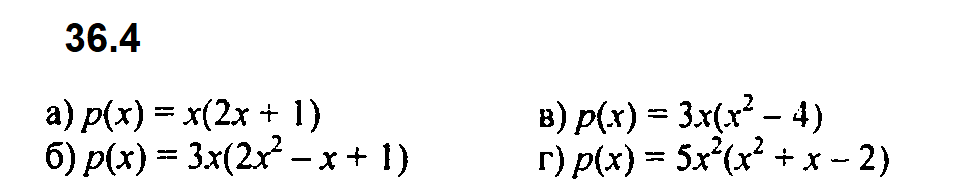
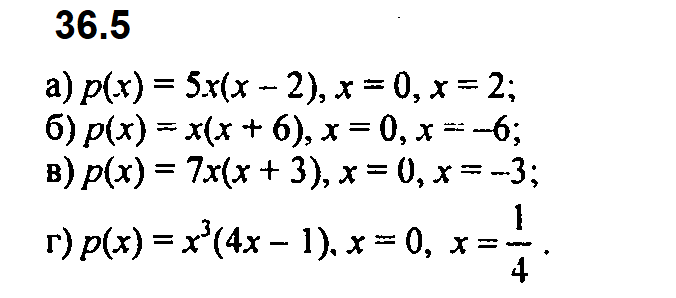
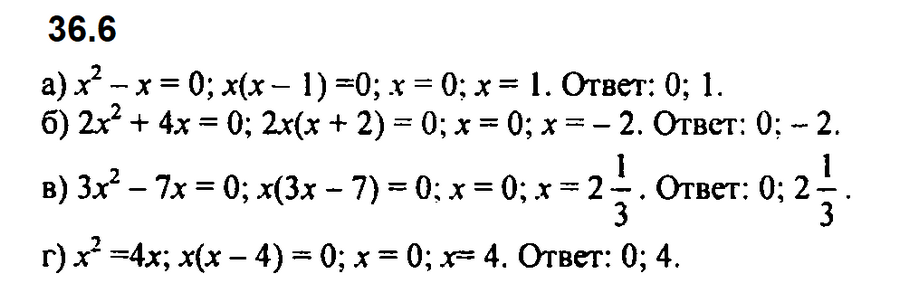
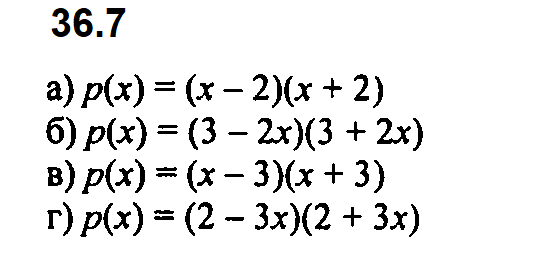
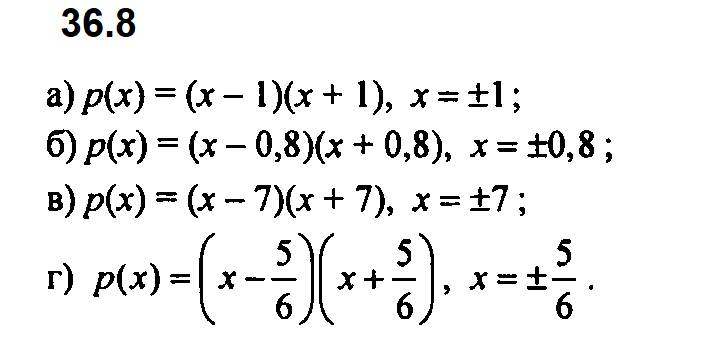
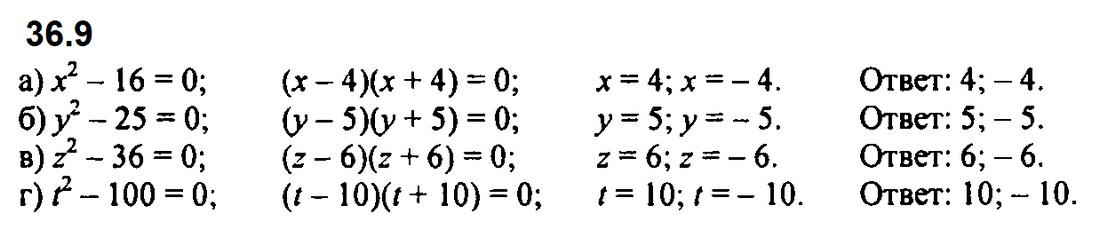
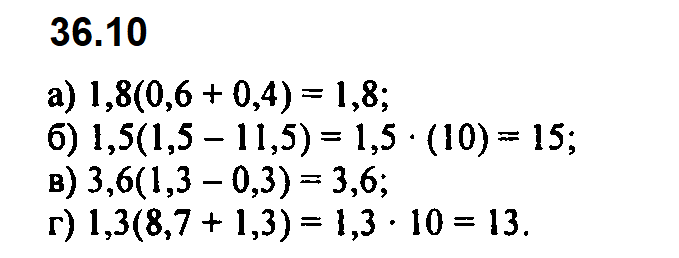
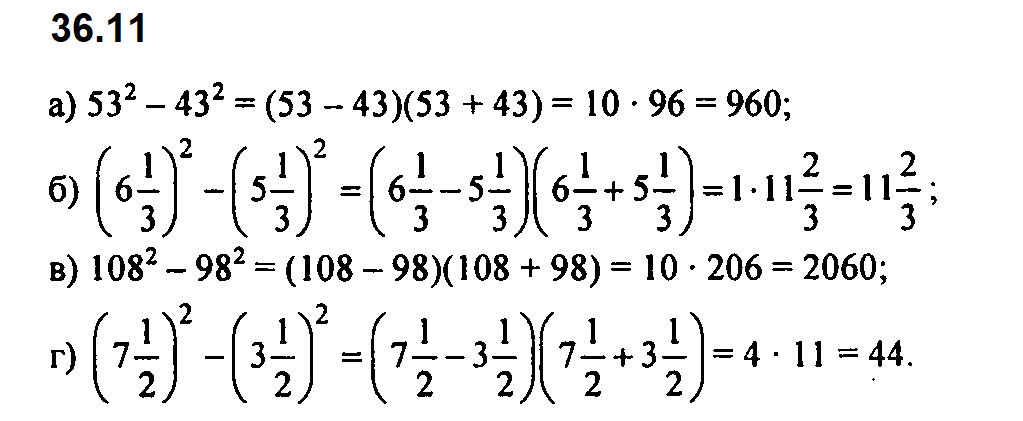


а где 36.19? Его же в письм. виде можно сделать.