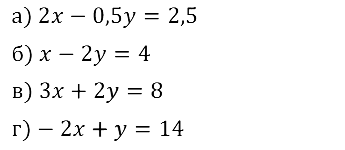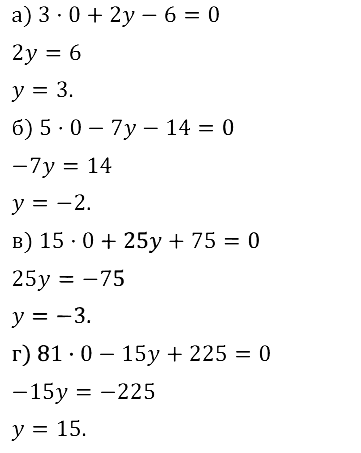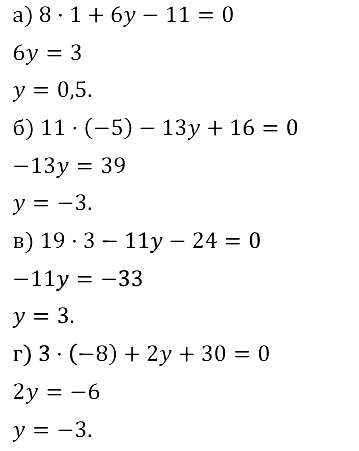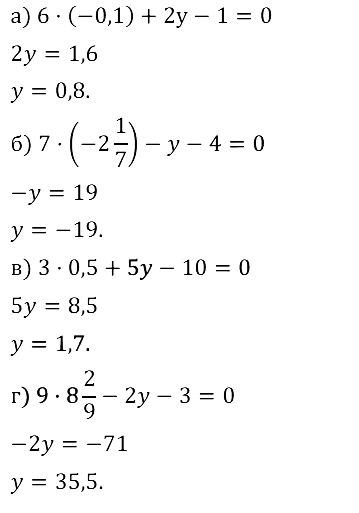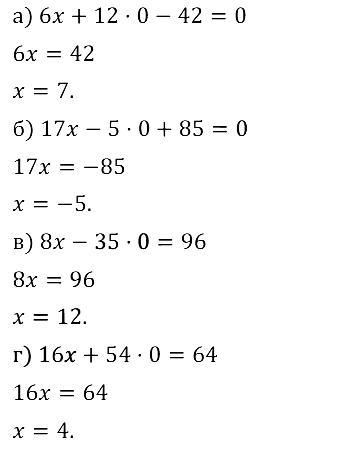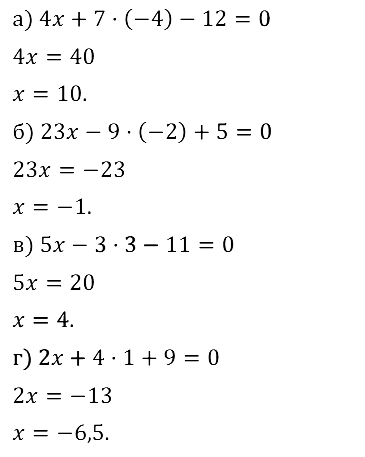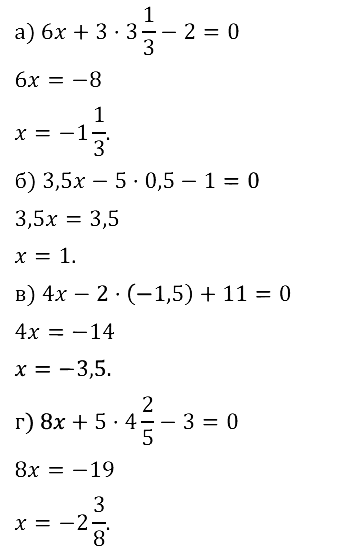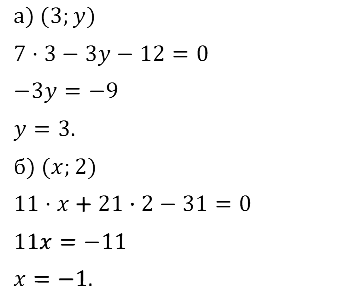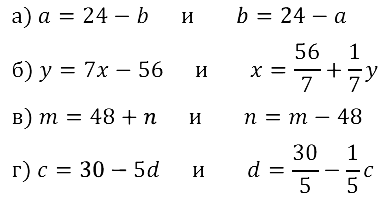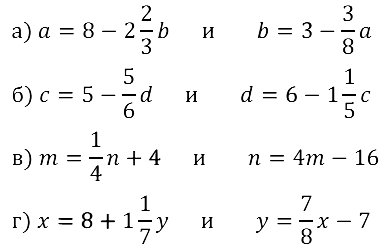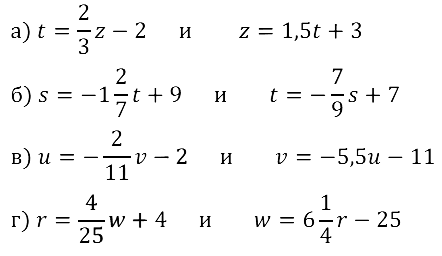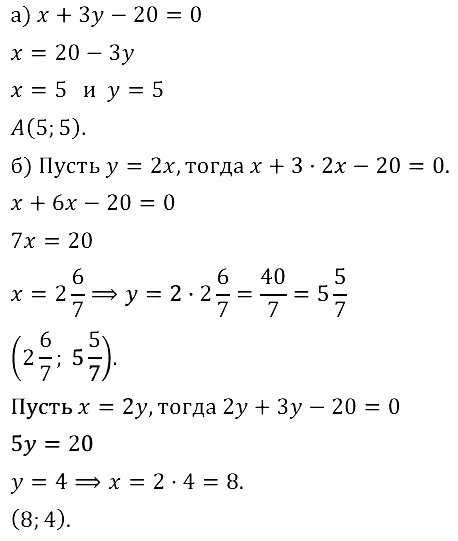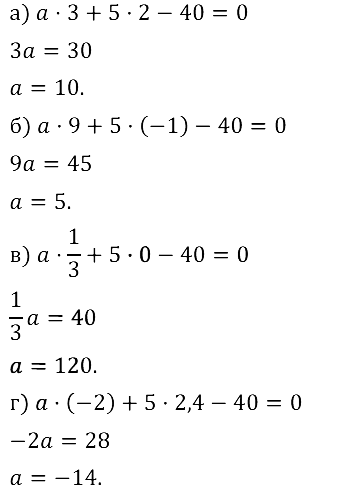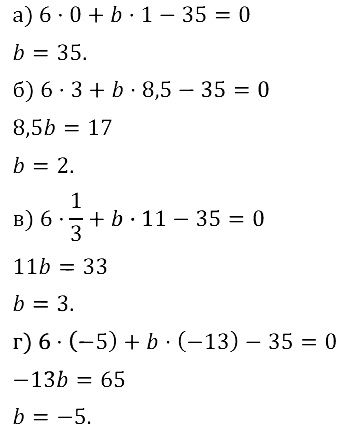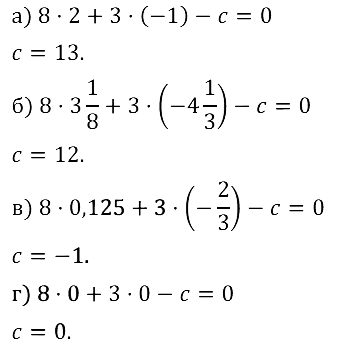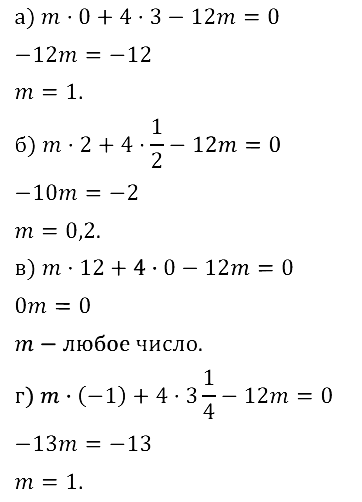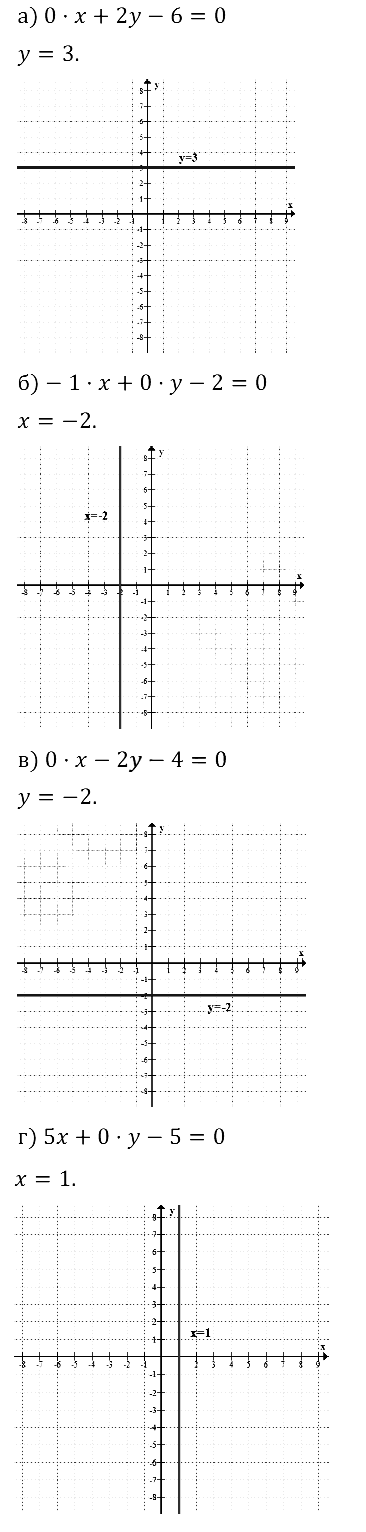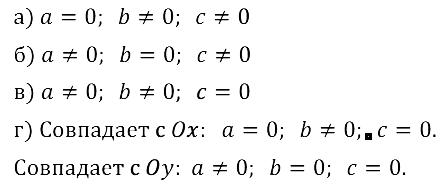ГДЗ Мордкович 7 (упр. 8.1 — 8.39). Алгебра 7 класс. Часть 2 Задачник. УМК Мордкович (Мнемозина, 2019-2021). Глава 2. Линейная функция. § 8. Линейное уравнение с двумя переменными и его график. Ответы на упражнения 8.1 — 8.39.
§ 8. Часть 1-я ОГЛАВЛЕНИЕ учебника § 8. Часть 2-я
Алгебра 7 Мордкович (упр. 8.1 — 8.39)
§ 8. Линейное уравнение с двумя переменными и его график
Задание № 8.1. Является ли линейным заданное уравнение с двумя переменными:
а) 5x + 3у + 7 = 0; в) 12с – 17d – 3 = 0;
б) 6а – 4b – 1 = 0; г) 45t + 4s + 19 = 0?
Задание № 8.2. Объясните, почему заданное уравнение не является линейным уравнением с двумя переменными: а) 3х2 + 5у – 1 = 0; б) 8х – 7у2 + 2 = 0.
Задание № 8.3. Является ли заданное уравнение с двумя переменными линейным:
а) x/3 + у – 5 = 0; в) (x – y)/2 + 4 = 0;
б) 3/x + y – 5 = 0; г) xy + 3 = 0?
Задание № 8.4. Назовите коэффициенты а, b и с линейного уравнения (ах + by + с = 0) с двумя переменными:
а) х – у + 4 = 0; в) х – 1 – 2у = 0;
б) х – 2у = 0; г) (y – x)/3 = 1.
Задание № 8.5. Является ли решением уравнения 5x + 2y – 12 = 0 пара чисел:
а) (3; 2); б) (1; 3,5); в) (12; 5); г) (4; –4)?
Задание № 8.6. Является ли решением уравнения 7а – 5b – 3 = 0 пара чисел:
а) (2; 8); б) (1; 4/5); в) (15; 1); г) (8; 10,6)?
Задание № 8.7. а) Какая из пар чисел (6; 2), (0; 20), (4; 8), (6; 5) является решением уравнения 3х + у = 20?
б) Какая из пар чисел (2; 0), (1; 1), (2,5; 2,5), (7; 8) является решением уравнения 5х – у = 10?
Задание № 8.8. Составьте какое–нибудь линейное уравнение с двумя переменными, решением которого служит пара чисел: а) (2; 3); б) (–6; –5); в) (6; –5); г) (–7; 0).
Задание № 8.9. Не выполняя построения, ответьте на вопрос: какие из точек М(5; 7), N(0; 3,5), К(7; 0), L(2; 3) принадлежат графику уравнения х + 2у – 7 = 0?
Для каждого из данных линейных уравнений найдите значение у, соответствующее заданному значению х:
Задание № 8.10. 3х + 2у – 6 = 0, если х = 0;
5х – 7у – 14 = 0, если х = 0;
15х + 25у + 75 = 0, если х = 0;
81х – 15у + 225 = 0, если х = 0.
Задание № 8.11. 8х + 6у – 11 = 0, если х = 1;
11х – 13у + 16 = 0, если х = –5;
19х – 11у – 24 = 0, если х = 3;
3х + 2у + 30 = 0, если х = –8.
Задание № 8.12.
Для каждого из данных линейных уравнений найдите значение х, соответствующее заданному значению у:
Задание № 8.13. а) 6х + 12у – 42 = 0, если у = 0;
б) 17х – 5у + 85 = 0, если у = 0;
в) 8х – 35у = 96, если у = 0;
г) 16х + 54у = 64, если у = 0.
Задание № 8.14.
Задание № 8.15.
Задание № 8.16. а) Известно, что абсцисса некоторой точки прямой, заданной уравнением 7х – 3у — 12 = 0, равна 3. Найдите ординату этой точки.
б) Известно, что ордината некоторой точки прямой, заданной уравнением 11х + 21y – 31 = 0, равна 2. Найдите абсциссу этой точки.
На координатной плоскости хОу постройте график уравнения:
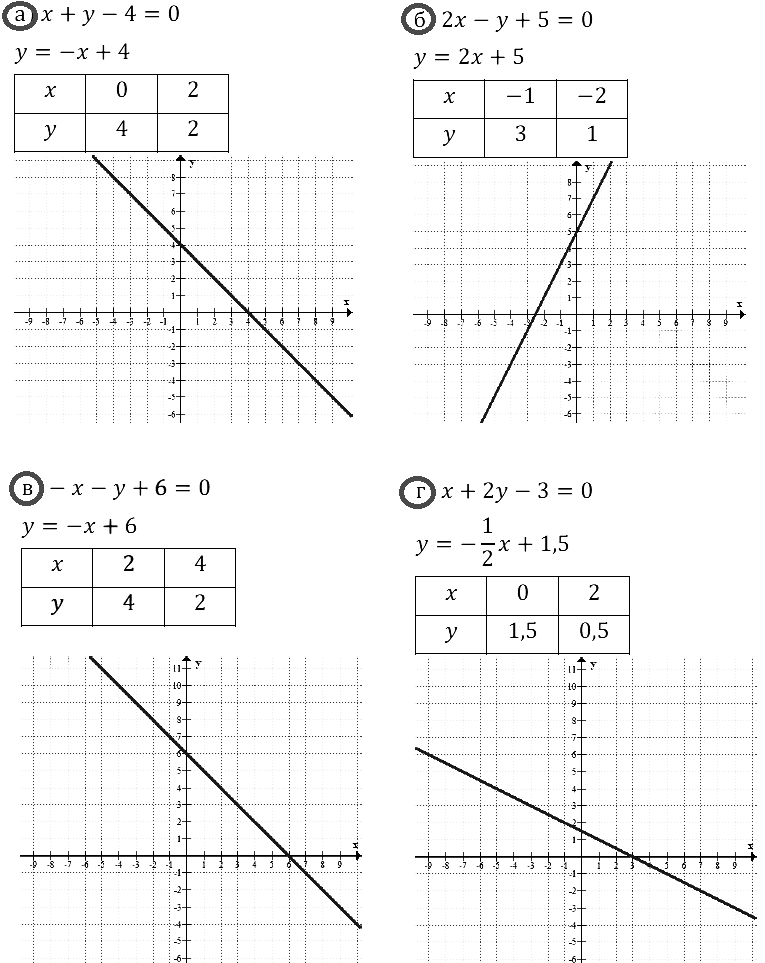
Задание № 8.17. а) х + у – 4 = 0; б) 2х – у + 5 = 0; в) –х – у + 6 = 0; г) х + 2y – 3 = 0.
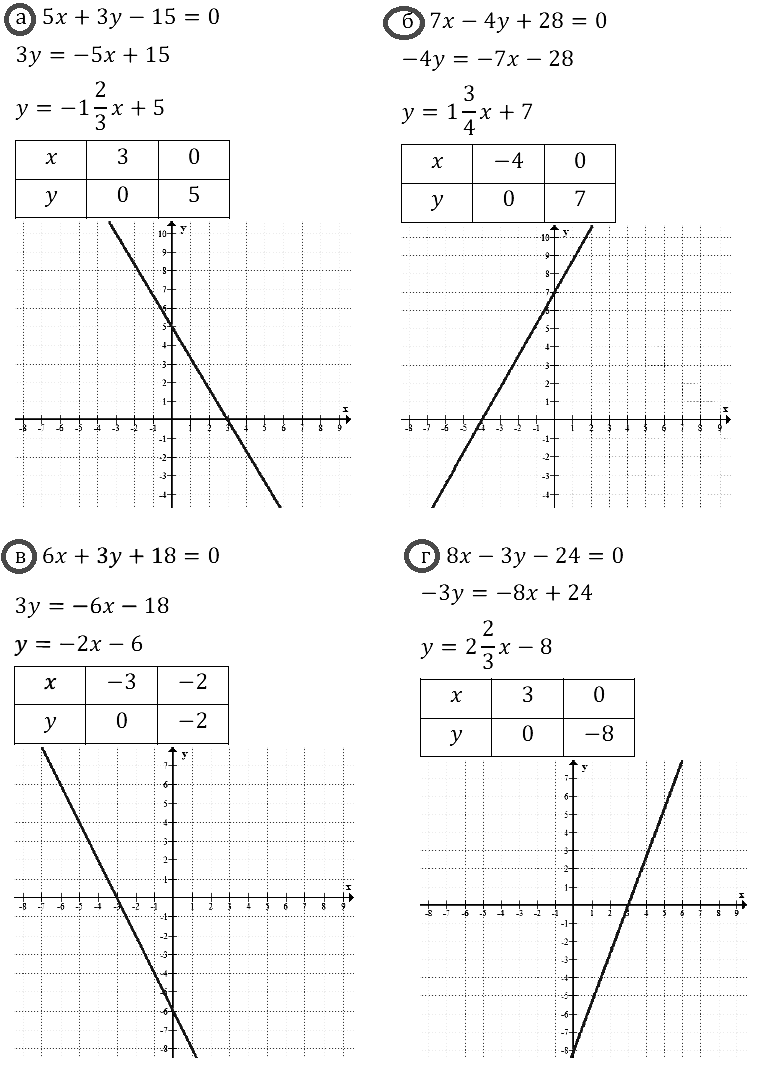
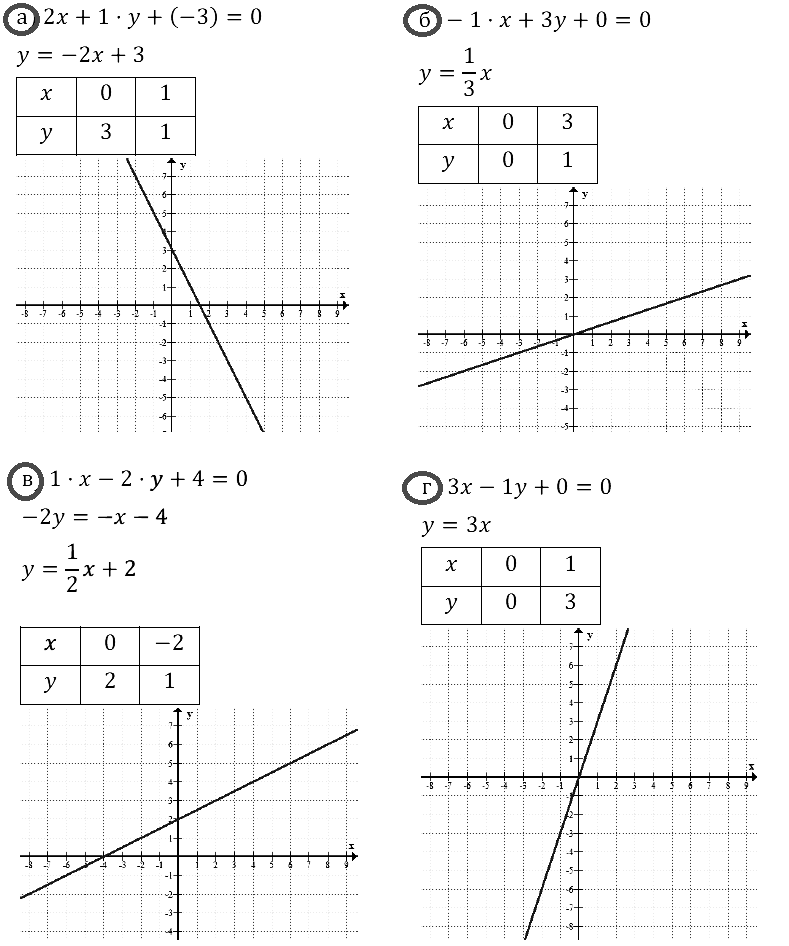
Задание № 8.18.
Задание № 8.19. На координатной плоскости tOs постройте график уравнения:
а) 7t + 9s + 63 = 0; в) 5t – 2s = 10;
б) 3t – 4s = 12; г) 4t + 9s + 36 = 0.
Задание № 8.20. а) Докажите, что прямые 5х + 11у = 8 и 10х — 7y = 74 пересекаются в точке А(6; –2).
б) Докажите, что прямые 12х – 7у = 2 и 4х – 5у = 6 пересекаются в точке В(–1; –2).
Задание № 8.21. Найдите координаты точки пересечения прямых:
а) х – у = –1 и 2х + у = 4; б) 4х + 3у = 6 и 2х + 3у = 0.
Дано линейное уравнение с двумя переменными. Используя его, выразите каждую из переменных через другую:
Задание № 8.22. а) а + b = 24; б) 7х – у = 56; в) m – n = 48; г) с + 5d = 30.
Задание № 8.23.
Задание № 8.24.
Задание № 8.25. Среди решений уравнения х + 3у – 20 = 0 найдите такую пару, которая состоит:
а) из двух одинаковых чисел; б) из двух таких чисел, одно из которых в 2 раза больше другого.
Задание № 8.26. Найдите значение коэффициента а в уравнении ах + 5y – 40 = 0, если известно, что решением уравнения является пара чисел: а) (3; 2); б) (9; –1); в) (1/3; 0); г) (–2; 2,4).
Задание № 8.27. Найдите значение коэффициента b в уравнении 6х + by – 35 = 0, если известно, что решением уравнения является пара чисел: а) (0; 1); б) (3; 8,5); в) (1/3; 11); г) (–5; –13).
Задание № 8.28. Найдите значение коэффициента с в уравнении 8x + 3y – с = 0, если известно, что решением уравнения является пара чисел: а) (2; –1); б) (3 1/8; –4 1/3); в) (0125; –2/3); г) (0; 0).
Задание № 8.29.
Решите задачу, использовав для составления математической модели две переменные и построив затем графики соответствующих линейных уравнений:
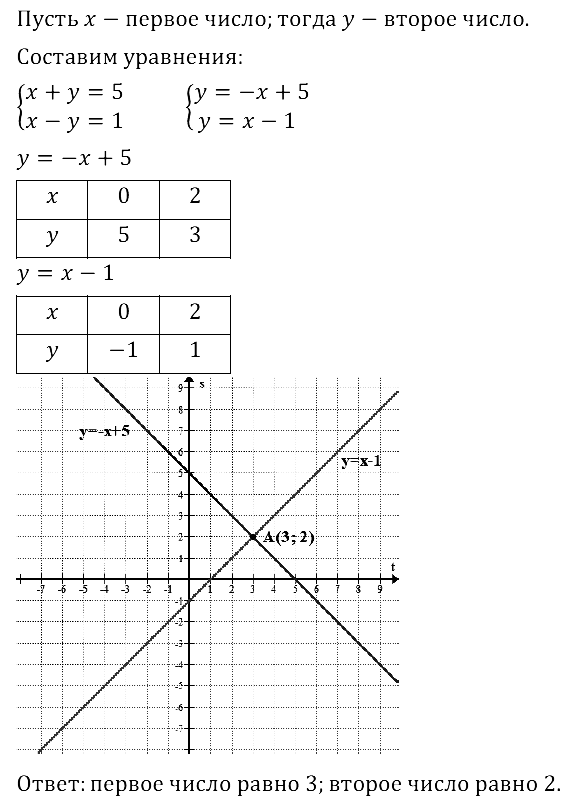
Задание № 8.30. Сумма двух чисел равна 5, а разность равна 1. Найдите эти числа.
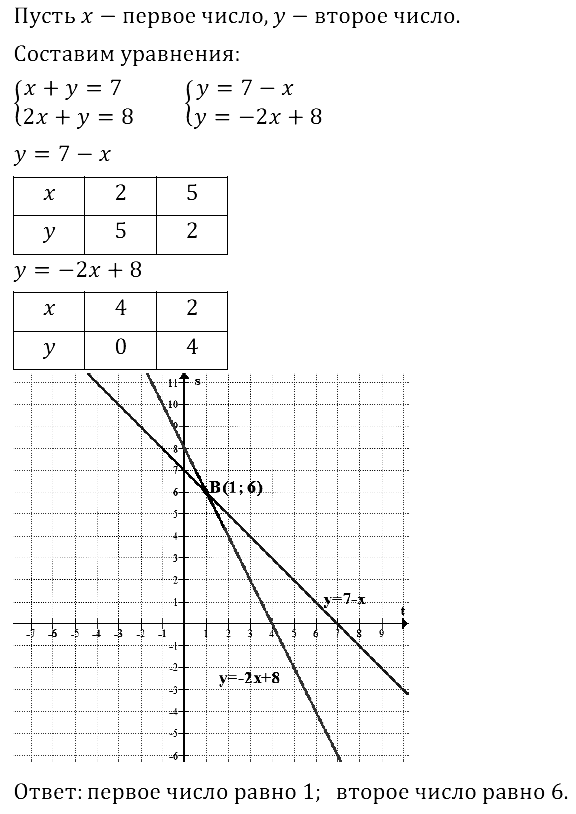
Задание № 8.31. Сумма двух чисел равна 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в сумме эти числа дадут 8. Найдите исходные числа.
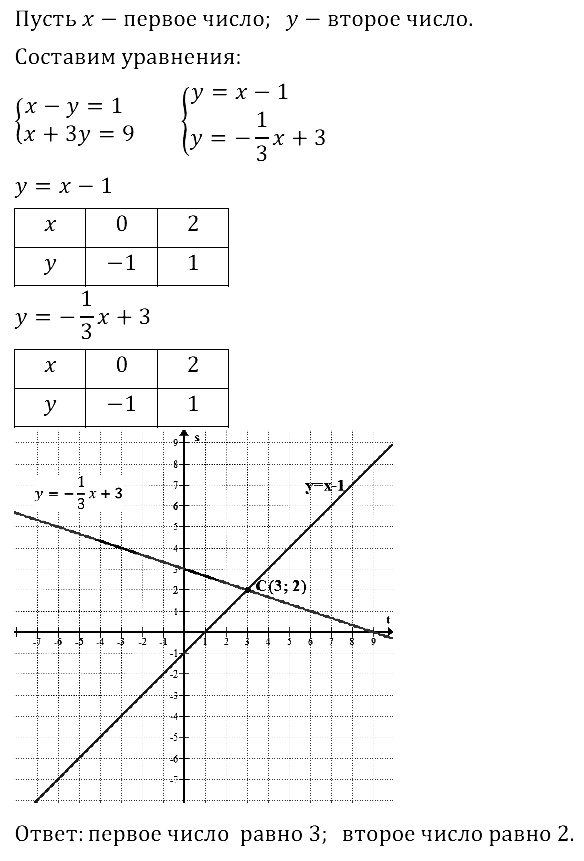
Задание № 8.32. Разность двух чисел равна 1. Если первое число оставить без изменения, а второе увеличить в 3 раза, то в сумме эти числа дадут 9. Найдите исходные числа.
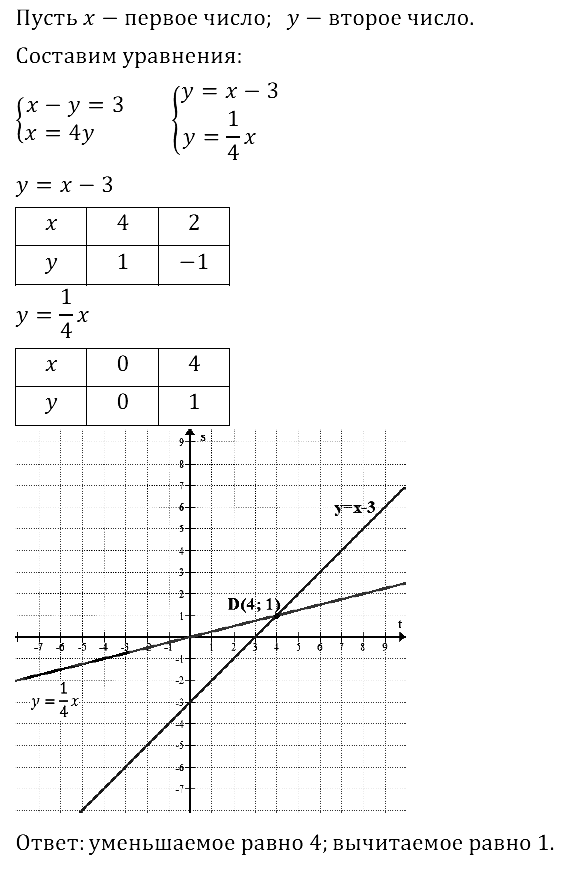
Задание № 8.33. Разность двух чисел равна 3. Найдите эти числа, если известно, что уменьшаемое больше вычитаемого в 4 раза.
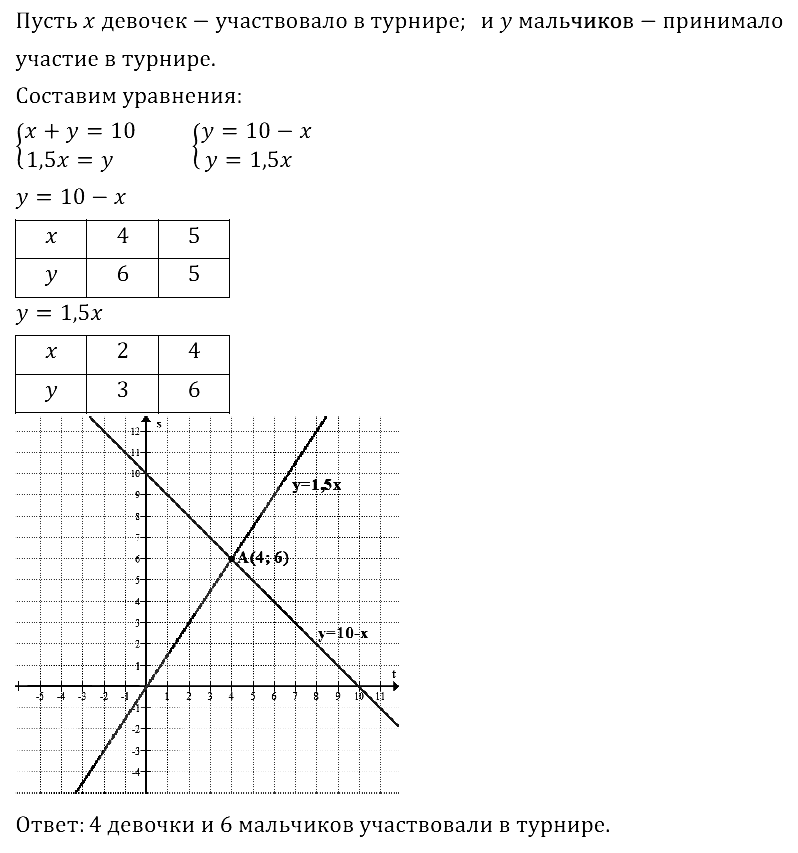
Задание № 8.34. В шахматном турнире участвовало 10 учеников. Мальчиков было в 1,5 раза больше, чем девочек. Сколько мальчиков и сколько девочек участвовало в турнире?
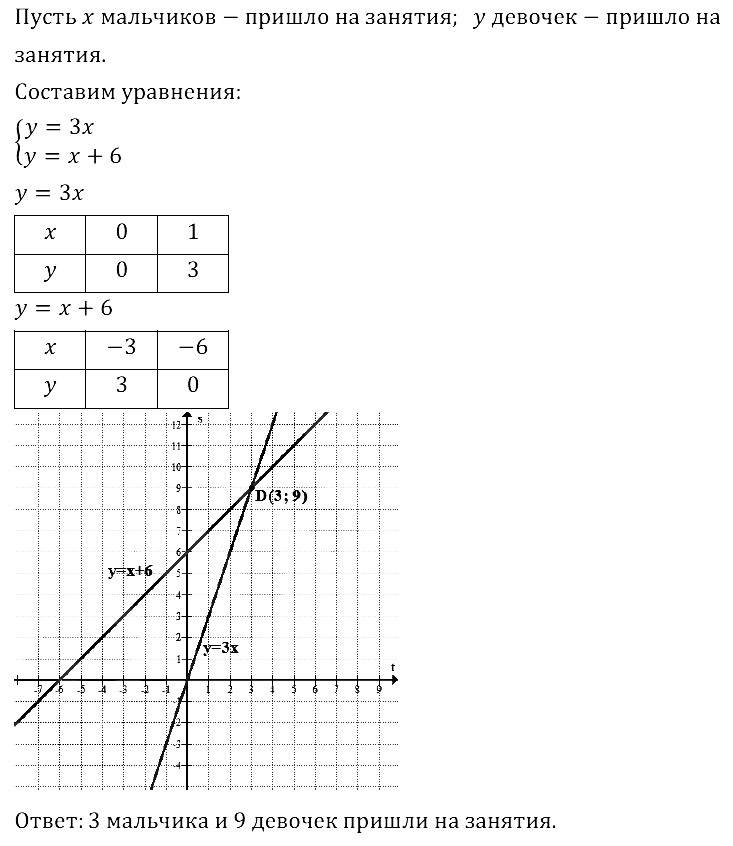
Задание № 8.35. На дополнительные занятия по математике девочек пришло в 3 раза больше, чем мальчиков. Сколько всего учеников пришло на дополнительные занятия, если мальчиков оказалось на 6 человек меньше, чем девочек?
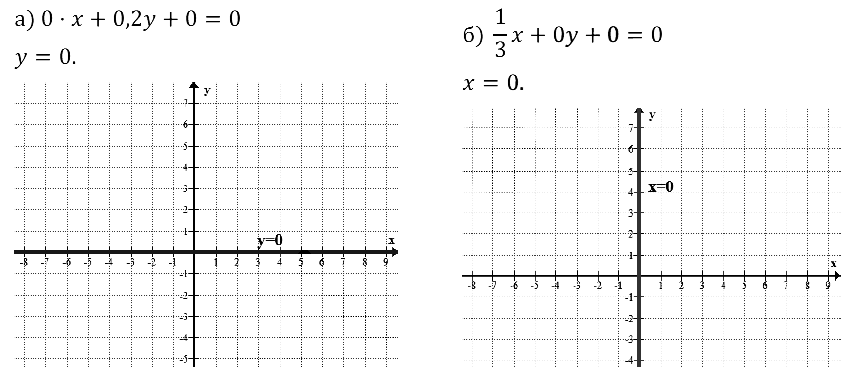
Задание № 8.36.
Задание № 8.37.
Задание № 8.38.
Задание № 8.39. При каких значениях коэффициентов а, b, с прямая ах + by + + с = 0:
а) параллельна оси х;
б) параллельна оси у;
в) проходит через начало координат;
г) совпадает с осью x, осью у?
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2021). Глава 2. Линейная функция. § 8. Линейное уравнение с двумя переменными и его график. Ответы на упражнения 8.1 — 8.39.