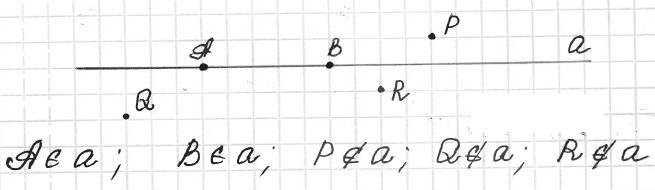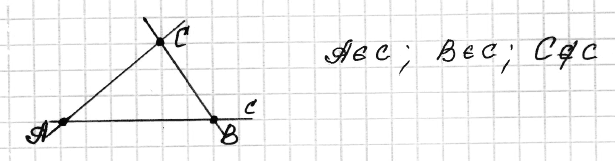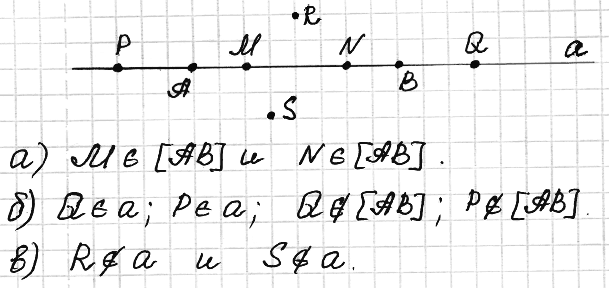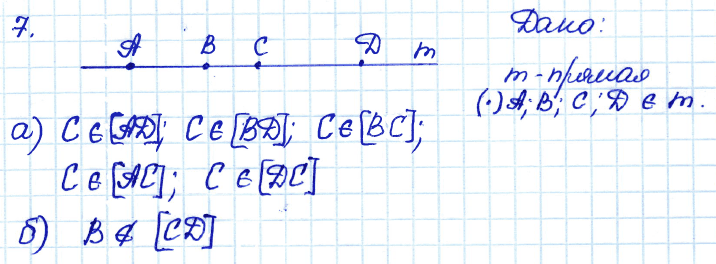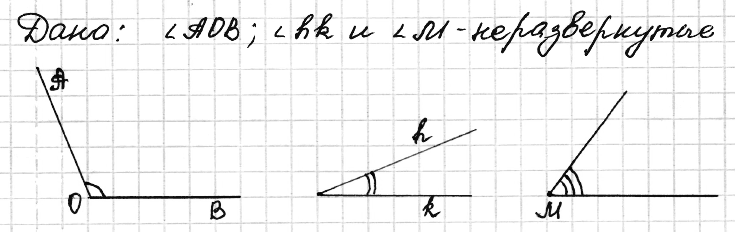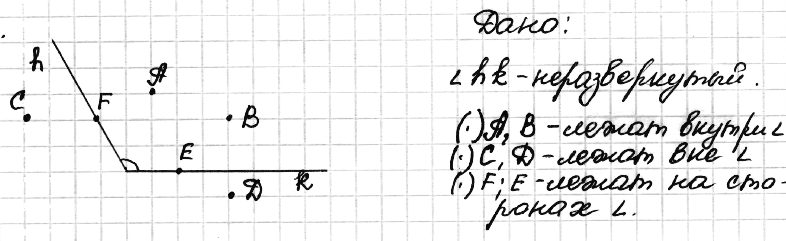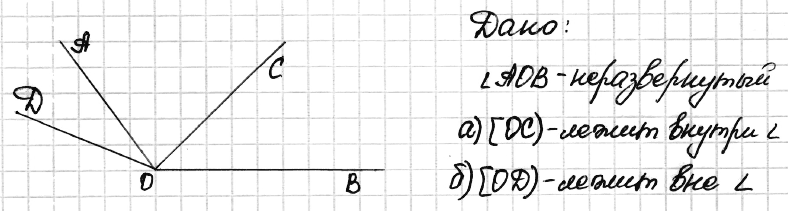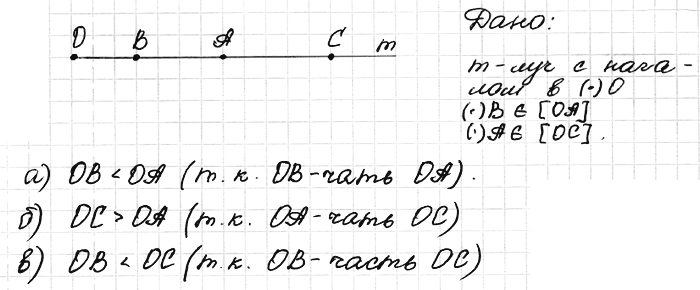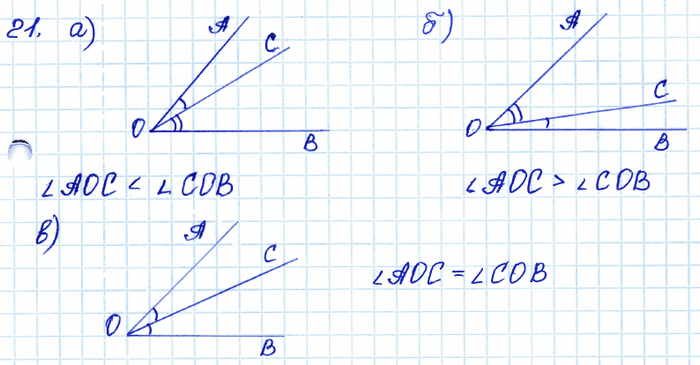Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения». Геометрия Атанасян Задачи 1-23 к:
- § 1. Прямая и отрезок (1. Точки, прямые, отрезки. 2. Провешивание прямой на местности)
- § 2. Луч и угол. (3. Луч. 4. Угол)
- § 3. Сравнение отрезков и углов. (5. Равенство геометрических фигур. 6. Сравнение отрезков и углов)
Вернуться в ОГЛАВЛЕНИЕ Смотреть задачи 24-40
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Геометрия 7 класс (УМК Атанасян)
Практические задания и задачи 1-23
Практические задания №№ 1-7
№ 1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
№ 2. □ Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.
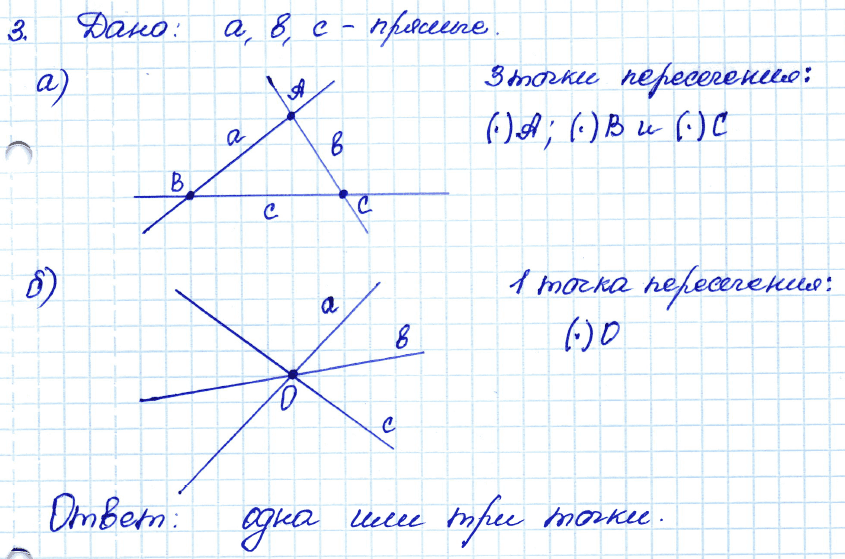
№ 3. Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
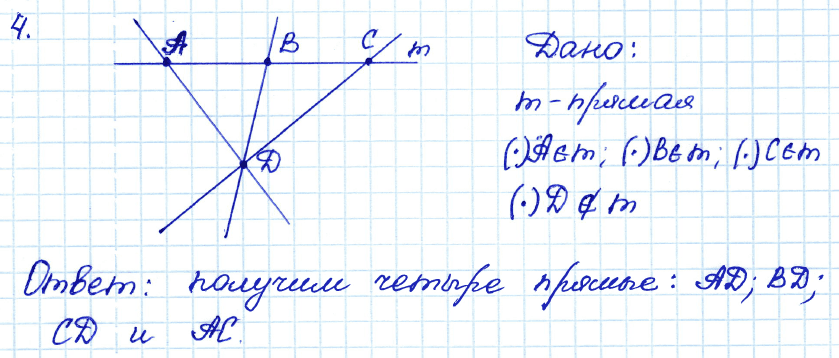
№ 4. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
№ 5. Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
№ 6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
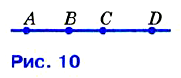№ 7. □ На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.
Практические задания №№ 8-17
№ 8. Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
№ 9. Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
№ 10. Начертите два развёрнутых угла и обозначьте их буквами.
№ 11. Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
№ 12. Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
№ 13. Начертите неразвёрнутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
№ 14. Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
№ 15. □ Сколько неразвёрнутых углов образуется при пересечении двух прямых?
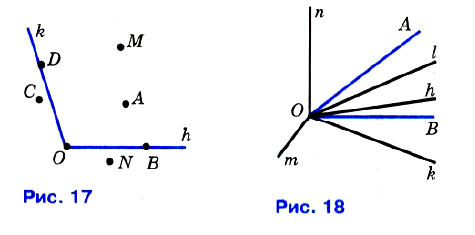
№ 16. □ Какие из точек, изображённых на рисунке № 17, лежат внутри угла hk, а какие — вне этого угла?
№ 17. Какие из лучей, изображённых на рисунке № 18, делят угол АОВ на два угла?
к § 3 «Сравнение отрезков и углов»
Задачи №№ 18-23
№ 18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
№ 19. Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
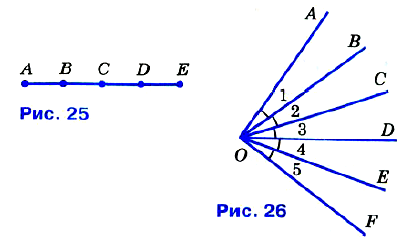
№ 20. □ На рисунке 25 отрезки АВ, ВС, CD и DE равны. Укажите: а) середины отрезков АС, АЕ и СЕ; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
№ 21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
№ 22. □ Луч l — биссектриса угла hk. Можно ли наложением совместить углы: a) hl и lk; б) hl и hk?
№ 23. □ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
Вы смотрели: Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения»: § 1. Прямая и отрезок; § 2. Луч и угол; § 3. Сравнение отрезков и углов. Геометрия Атанасян Задачи к Главе 1 задачи 1-23.