Ознакомительная версия с цитатами из учебника для принятия решения о покупке. Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — М.: Просвещение. ГЛАВА I учебника. § 1. ВЫРАЖЕНИЯ. (1. Числовые выражения. 2. Выражения с переменными. 3. Сравнение значений выражений. Упражнения №№ 1 — 69. Контрольные вопросы и задания. Дополнительные упражнения №№ 206 — 222 к параграфу 1)
ГДЗ Упр. 1 — 18 ГДЗ Упр. 19 — 46 ГДЗ Упр. 47 — 69
§ 1. ВЫРАЖЕНИЯ.
1. Числовые выражения
Решим задачу: «Туристы в течение двух часов ехали на велосипедах по шоссе со скоростью 16 км/ч, а затем шли лесом ещё 7 км. Какова длила всего маршрута?»
По шоссе туристы проехали 16 • 2 км, а лесом прошли 7 км. Поэтому длина всего маршрута равна (16 • 2 + 7) км, т. е. 39 км. Решая задачу, мы получили числовое выражение 16 • 2 + 7. Числовые выражения составляются из чисел с помощью знаков действий и скобок. Приведём ещё примеры числовых выражений:
43 : 5; 9,6 – 3 • 1,2; 5 • (7,4 – 6,1).
Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения.
Найдём, например, значение выражения 12 • 6 – 35 : 7. Для этого мы должны, соблюдая принятый порядок действий, выполнить сначала умножение и деление, а затем вычитание:
1)12 • 6 = 72; 2) 35 : 7 = 5; 3) 72 – 5 = 67.
Число 67 – значение выражения 12 • 6 – 35 : 7.
Если в выражении встречается деление на нуль, то это выражение не имеет числового значения, так как на нуль делить нельзя. О таких выражениях говорят, что они не имеют смысла.
Например, не имеют смысла такие выражения, как 35 : (4 • 2 – 8), 1/(12 + 4 • (–3))
Упражнения №№ 1 — 18
- Найдите значение выражения:
а) 6,965 + 23,3; г) 6,5 • 1,22; ж) 53,4 : 15;
б) 50,4 – 6,98; д) 0,48 • 2,5; з) 16,94 : 2,8;
в) 88 – 9,804; е) 0,016 • 0,25; и) 75 : 1,25. - Выполните действия:
а) 481,92 : 12 – 20,16; б) 1,08 • 30,5 – 9,72 : 2,4 - Найдите значение выражения:
а) 3,6 : 0,08 + 5,2 • 2,5; б) (9,885 – 0,365) : 1,7 + 4,4. - Выполните действие:
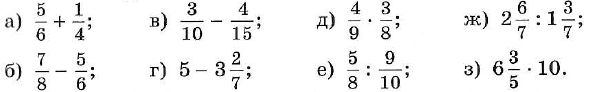
- Выполните действие:
а) 4,2 – 8; г) 1,2 • (–5); ж) 38 : (–0,19);
б) –2,4 + 5,6; д) –8 • 4,5; з) –16 : 0,2;
в) –2,1 – 3,2; е) –0,9 • (–0,1); и) –6,4 : (–8). - Вычислите:
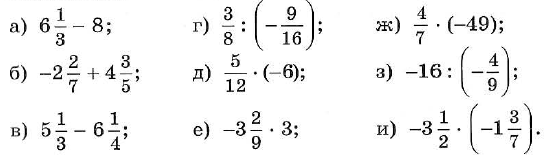
- Найдите:
а) 1% числа 240; в) 120% числа 8;
б) 40% числа 15; г) 9,5% числа 280. - На пакете молока написано, что в молоке содержится 3,2% жира, 2,5% белка и 4,7% углеводов. Какое количество каждого из этих веществ содержится в стакане (200 г) молока?
- В фермерском хозяйстве собирали по 36 ц пшеницы с гектара. Применение интенсивной технологии позволило увеличить производство пшеницы на той же площади на 25%. Сколько центнеров пшеницы стали собирать с 1 га в этом фермерском хозяйстве?
- За несколько книг уплатили 320 р. Стоимость одной из книг составила 30%, а другой – 45% израсходованных денег. На сколько рублей первая книга дешевле второй?
[11.] Используя три раза цифру 2, составьте выражение, значение которого равно: а) 6; б) 8; в) 3; г) 1.
- Составьте какое–нибудь выражение, содержащее два знака действия, значение которого равно: а) 12; б) 0.
- Из данных выражений выберите выражение, не имеющее смысла.
1. 126 : (36 • 2 – 5 • 8) 3. (1,7 • 2 – 3,4) : 11 - (2,6 – 13 • 0,2) / 8 4. 0,57 / (0,8 – 0,4 • 2)
- Составьте какое–либо выражение, не имеющее смысла.
- Составьте числовое выражение для решения задачи: «Из двух населённых пунктов, расстояние между которыми 40 км, вы шли, одновременно навстречу друг другу два пешехода. Какое расстояние будет между ними через 3 ч, если известно, что скорость одного пешехода 4 км/ч, а скорость другого пешехода 5 км/ч?»
- Решите задачу, составив выражение: «Один рабочий изготовляет за час 7 деталей, а другой – 9 деталей. Сколько деталей они изготовят за 4 ч?»
- Используя термины «сумма», «разность», «произведение» «частное», прочитайте выражение:
а) 8,5 – 7,3; б) 4,7 • 12,3; в) 65 : 1,3;
г) 5,6 + 0,9; д) 2 • 9,5 + 14; е) (10 – 2,7) : 5;
ж) 6,1 • (8,4 : 4); з) (6,4 + 7) : 2; и) 2,5 – (3,2 + 1,8);
к) (5,74 – 1,24) • 3,6; л) 8 – (1,71 + 0,19); м) 0,36 : 0,3 – 1,78.
(Задача исследование.) Из 36 учащихся класса каждый изучает хотя бы один иностранный язык – английский или немецкий. Известно, что 25 учащихся изучают английский язык, а 20 учащихся – немецкий язык. Сколько процентов всех учащихся изучают оба языка?
1) Укажите число учащихся, изучающих хотя бы один из этих языков.
2) Вычислите число учащихся, изучающих оба языка – английский и немецкий.
3) Найдите, сколько процентов учащихся изучают оба языка.
2. Выражения с переменными
Двигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за 3 ч – 60 • 3 км, за 5 ч – 60 • 5 км, за 5,5 ч – 60 • 5,5 км. Вообще за t ч он пройдёт 60t км. Изменяя значение t, мы можем с помощью выражения 60t находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t – выражением с переменной.
Приведём ещё пример. Пусть длины сторон прямоугольника равны а см и b см. Тогда его площадь равна аb см2. Выражение аb содержит две переменные а и b. Оно показывает, как находить площадь прямоугольника при различных значениях а и b. Например:
если а = 8 и b = 11, то аb = 8 • 11 = 88;
если а = 25 и b = 4, то ab = 25 • 4 = 100.
Если в выражение с переменными подставить вместо каждой переменной какое–либо её значение, то получится числовое выражение. Его значение называют значением выражения с переменными при выбранных значениях переменных.
Так, число 88 есть значение выражения ab при а = 8 и b = 11, число 100 есть значение этого выражения при а = 25 и b = 4.
Рассмотрим выражение b/(b–3). При любом b ≠ 3 можно найти его значение. Например, если b = 13, то b/(b–3) = 13/(13–3) = 13/10 = 1,3
При b = 3 значение этого выражения найти нельзя, так как в этом случае делитель b–3 равен нулю. Говорят, что при b ≠ 3 выражение b/(b–3) имеет смысл, а при b = 3 оно не имеет смысла.
Некоторые выражение имеют смысл при всех значениях переменных. Примерами могут служить выражения:![]()
Выражения с переменными используются для записи формул.
Рассмотрим примеры. Любое чётное число m можно представить в виде произведении числа 2 и целого числа n, т. е. m = 2n.
Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут чётные числа. Формулу m = 2n называют формулой чётного числа.
Формулу m = 2n + 1, где n – целое число, называют формулой нечётного числа. Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу. Например, формулу числа, кратного 3, можно записать так: m = 3n, где n – целое число.
Упражнения №№ 19 — 46
- Найдите значения выражения:
а) 4х – 12 при х = 7; 0; –5; б) 2,8 – 0,5у при у = 3; 0; –6. - Заполните таблицу, вычислив значения выражений Зх – 1 и –Зх + 1 для указанных значений х:
| x | –2 | –1 | 0 | 1 | 2 | 4 | 5 |
| 3х – 1 | |||||||
| –3х + 1 |
Какими числами являются соответственные значения выражений Зх – 1 и –Зх + 1?
- Найдите значения выражений 10 – 2у и 10 + 2у и запишите их в соответствующие клетки таблицы:
| у | –3 | –1 | 0 | 2 | 3 | 4 | 6 |
| 10 – 2у | |||||||
| 10 + 2у |
- Какие значения принимают сумма х + у и произведение ху при следующих значениях переменных:
а) х = 1,2, у = –2,5; в) х = 0,1, у = 0,2;
б) х = –0,8, у =3, г) х = –1,4, у = –1,6? - Найдите значение выражения 5m – 3n, если:
а) m = –2/5, n = 2/3; б) m = 0,2, n = –1,4. - Вычислите значение выражения х/2 – у, если:
а) х = 2,4, у = 0,8; в) х = 4,8, у = –2,1;
б) х = –3,6, у = 5; г) х = –4,4, у = –3. - Заполните таблицу, вычислив значения выражения а – 2b:
| а | 5 | –2 | 4 | 1 | 6 |
| b | –3 | 3 | 0 | –1 | 4 |
| а – 2b |
- Известно, что при некоторых значениях х и у значение выражения х – у равно 0,7. Какое значение принимает при тех же х и у выражение:
а) 5 (х – у); б) у – х; в) 1/(х–у); г) (х–у)/(у–х)? - Известно, что при некоторых значениях а и b значение выражения а – b равно 4. Чему равно при тех же а и b выражение 12/(b–a) + 16/(b–a)2? Выберите верный ответ.
1. –2 2. 2 3. –4 4. 4 - Вычислите значение выражения:
а) ах – 3у при а = 10, х = –5, у –1/3
б) ах + bх + с при а = 1/2; х = 2, b = –3, с = 5,8. - Опытное поле разбили на два участка. Площадь первого участка а га, а второго – b га. С каждого гектара первого участка собрали 32 ц пшеницы, а с каждого гектара второго участка собрали 40 ц. Сколько пшеницы собрали с обоих участков? Вычислите при а = 120 и b = 80.
- На стройке работало 5 бригад, по а человек в каждой, и 3 бригады, по b человек в каждой. Сколько человек работало на стройке? Вычислите при а = 25 и b = 32.
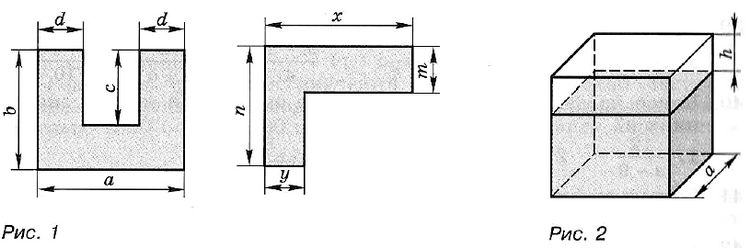
- На рисунке 1 указаны длины отрезков (в сантиметрах). Для каждой фигуры составьте выражение для вычисления её площади (в квадратных сантиметрах).
- Ребро куба равно а м. От этого куба отрезан прямоугольный параллелепипед, высота которого равна h м (рис. 2). Найдите объём оставшейся части.
- В 250 г водного раствора соли содержалось х г соли. Какой стала концентрация раствора после добавления в него 5 г соли? Выберите верный ответ.
- В сплаве олова и свинца массой 20 кг содержалось х кг олова. Каким стало процентное содержание олова в сплаве после добавления в него 2 кг олова?
- Длина прямоугольника а см, ширина b см. Что означает выражение: a) ab; б) 2а + 2b; в) а + b; г) 2а?
- Тетрадь стоит х р., а карандаш стоит у р. Что означает выражение: а) х + у; б) Зх + у; в) 2х + 3у; г) x/y?
- Прочитайте, пользуясь терминами «сумма», «разность», «про изведение» и «частное», выражение:
а) mx; в) (а + 5)х; д) 2х + 1; ж) ab + bс;
б) 10 + ab; г) m – 8а; е) a/b + с; з) (а – b)(а + b). - Запишите в виде выражения: а) сумму чисел b и с; б) разность чисел а и m; в) квадрат числа х; г) куб числа у; д) сумму числа х и произведения чисел а и b; е) разность числа m и частного чисел х и у; ж) произведение суммы чисел а и b и числа с; з) произведение числа а и суммы чисел х и у.
- При каких выражениях переменной имеет смысл выражение:
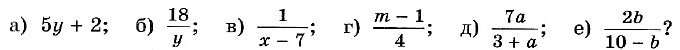
- Какое из данных выражений имеет смысл при любых значениях а?

- Составьте формулу числа: а) кратного 5; б) кратного 10; в) кратного 101,
- Напишите формулу числа, кратного 7. Найдите по этой формуле два трёхзначных числа, кратных 7.
- (Для работы в парах.) Докажите, что всякое простое число, начиная с 5, увеличенное или уменьшенное на 1, делится на 6.
1) Проверьте утверждение на примерах. Одному учащемуся рекомендуем взять простые числа из третьего десятка, другому – из седьмого десятка.
2) Обсудите друг с другом, из чего следует справедливость указанного свойства.
3) Проведите доказательство. - Найдите число, если известно, что: а) 3% этого числа равны 1,8; б) 85% этого числа равны 17; в) 130% этого числа равны 3,9; г) 6,2% этого числа равны 9,3.
- После того как из бидона отлили 30% молока, в нём осталось 14 л. Сколько литров молока было в бидоне первоначально?
- Перевыполнив план на 15%, завод выпустил за месяц 230 станков. Сколько станков должен был выпустить за месяц завод по плану?
3. Сравнение значений выражений
Решим задачу: «Пшеницей засеяли два опытных участка площадью 48 га и 60 га. С первого участка собрали 1800 ц пшеницы, а со второго 2100 ц. На каком участке урожайность выше?»
Урожайность выражается частным от деления массы пшеницы, собранной с участка, на площадь участка. Чтобы узнать, на каком участке урожайность выше, надо сравнить значения выражений 800 : 48 и 2100 : 60. Так как 1800 : 48 = 37,5; 2100 : 60 = 35, то урожайность выше на первом участке.
Для любых двух числовых выражений можно установить, равны их значения или нет, и если они не равны, то какое из них больше и какое меньше.
Результат сравнения значений выражений можно записать в виде равенства или неравенства. Например, результат сравнения частных 1800 : 48 и 2100 : 60 можно записать в виде неравенства: 1800 : 48 > 2100 : 60.
Если выражения содержат переменные, то для разных значении переменных результат сравнения значений этих выражений может оказаться различным.
Сравним, например, значения выражений 2а и а + 4 при а = 0; 4; 10.
- Если а = 0, то 2а = 0 и а + 4 = 4, т. е. при а = 0 верно неравенство 2а < а + 4.
- Если а = 4, то 2а = 8 и а + 4 = 8, т. е. при а = 4 верно равенство 2а = а + 4.
- Если а = 10, то 2а = 20 и а + 4 = 14, т. е. при а = 10 верно неравенство 2а > а + 4.
Иногда требуется установить, между какими числами заключено значение выражения.
Рассмотрим пример. Пусть при взвешивании металлического шарика установили, что его масса больше 86 г, но меньше 87 г. Обо значим массу шарика (в граммах) буквой m. Тогда результат взвешивания можно записать так: m > 86 и m < 87, или иначе: 86 < m и m < 87.
Два неравенства 86 < m и m < 87 можно записать в виде двойного неравенства 86 < m < 87.
Неравенство 86 < m < 87 читают так: «86 меньше m и m меньше 87» – или короче: «m больше 86 и меньше 87».
Рассмотрим ещё один пример. Число дней в месяце меньше 31 или равно 31. Обозначим число дней в месяце буквой n. Тогда n < 31 или n = 31. Вместо этой записи обычно пишут одно неравенство n ≤ 31 (читают: «n меньше или равно 31»).
Число дней в месяце больше или равно 28: n > 28 или n = 28. В таких случаях также пишут короче: n ≥ 28 (читают: «n больше или равно 28»).
Так как n ≥ 28, то 28 ≤ n.
Два неравенства 28 ≤ n и n ≤ 31 можно записать в виде двойного неравенства 28 ≤ n ≤ 31.
Неравенства, составленные с помощью знаков > и <, называют строгими неравенствами, а неравенства, составленные с помощью знаков ≥ и ≤ называют нестрогими.
Упражнения №№ 47 — 69
- Сравните значения выражений:
а) 2,06 • 3,05 и 21,28 : 3,5; в) 1/2 + 1/5 и 1/3 + 1/4;
б) 97,2 : 2,4 и 62 – 21,6; г) 16 – 3 5/8 и 15 – 2 1/4 . - Сравните значения выражений, не вычисляя их:
а) 56 • 2/7 и 56 : 7/2; в) 2,1 – 5,8 и 2,1 – 1,7;
б) 9 : 0,6 и 9 • 0,6; г) 6,13 – 7,57 и –6,13 + 7,57. - Сравните значения выражений, не вычисляя их:
а) 6,16 – 7,44 и 7,23 + 8,11; в) 5,7 – 3,11 и 5,7 – 2,16;
б) 24,12 • 1/4 и 24,12 : 1/4; г) 65,4 • 5/6 и 65,4 : 5/6. - Сравните значения выражений: а) 0,7 • 0,8 • 0,9 и 0,7 + 0,8 – 0,9; б) 1/2 + 1/3 – 1/6 и 1/2 • 1/3 • 1/6.
- Сравните значения выражений:
а) 9,5 – а и 0,5а при а = 3,8; 0; 5;
б) 3 – с и 4с – 5 при с = 1,6; –3; –6. - Сравните значения выражений: а) х и –х при х = 8; 0; –3; б) х и 100х при х = 5; 0; –5.
- Сравните значения выражений:
а) 5m – 0,8 и 0,8m – 5 при m = –1;
б) аb и а : b при а = 4,6, b = 0,23. - Верно ли неравенство 2х + 5 < Зх при х = 4,2; 5; 6,5?
- Прочитайте неравенство:
а) 8,1 < 8,14 < 8,6; г) –40 <–38,7 <–30;
б) 9 < 9,865 < 10; д) 1 3/5 < 1,7 < 1 4/5;
в) –900 < –839 < –800; е) 2,42 < 2 3/7 < 2,43. - Запишите в виде двойного неравенства:
- а) 8 меньше 13 и 13 меньше 15;
- б) 4,1 меньше 4,18 и 4,18 меньше 4,2;
- в) 63,5 больше 63 и меньше 64;
- г) –8,1 больше –11 и меньше –7;
- д) а больше 1,8 и меньше 2,8;
- е) х больше а и меньше b.
- Подберите какое–нибудь число, заключённое между числами:
а) 8,6 и 8,7; б) 1/7 и 1/8; в) –3,6 и –3,7; г) 3/4 и 5/6.
Результат запишите в виде двойного неравенства. - Запишите в виде двойного неравенства:
а) 0,79 больше 0,7 и меньше 0,8;
б) 6 4/5 больше 6 и меньше 7;
в) –4,6 больше –10 и меньше 0;
г) m больше –16 и меньше –15;
д) k больше 2,65 и меньше 2,66;
е) у больше m и меньше n. - На координатной прямой точками отмечены числа а, b и c (рис. 3). Укажите для каждой точки соответствующее ей число, если известно, что а > b и с > а. Составьте из чисел а, b и с двойное неравенство с помощью знака <.

- Прочитайте неравенство:
а) 7,3 ≤ x; г) k ≤ 0,5; ж) –5 ≤ а < –2;
в) у ≥ 0,83; д) 4,4 ≤ n ≤ 6,1; з) х ≤ b ≤ у.
в) а ≥ –10,4; е) 7,6 ≤ m ≤ 20,8; - Верно ли неравенство:
а) х ≤ 5,3 при х = 2,7; 5,3; 6;
б) у ≥ 4,8 при у = 3,5; 4,8; 7,1;
в) 0,6 < х ≤ 0,8 при х – 0,5; 0,6; 0,7; 0,8; 0,9;
г) 2,1 ≤ у ≤ 2,4 при у = 2,1; 2,2; 2,3; 2,4; 2,5? - Запишите с помощью знаков неравенства:
а) х меньше или равно 8;
б) у больше или равно 0;
в) а больше 5 и меньше или равно 7;
г) b больше или равно –2 и меньше 1, - Запишите в виде неравенства:
а) х – отрицательное число;
б) m – положительное число;
в) у – неотрицательное число;
г) z – неположительное число. - Запишите в виде двойного неравенства:
а) х больше или равно 11 и меньше 12;
б) у больше 50 и меньше или равно 100;
в) а больше 350 и меньше 400;
г) b больше или равно –100 и меньше или равно –10. - Один автомобиль прошёл 700 км за х ч, а другой автомобиль прошёл 630 км за у ч. Сравните средние скорости автомобилей, если: а) х = 12,5, у = 10,5; б) х – у = 14.
- Сколько процентов составляет: а) число 8 от числа 200; б) число 2,1 от числа 14?
- В результате рационализации производства удалось сократить число рабочих на комбинате. Вместо 1600 их осталось 1200. На сколько процентов сократилось число рабочих?
- Найдите значение выражения:
а) 37,6 – 5,84 + 3,95 – 8,9; в) 17,1 • 3,8 : 4,5 • 0,5;
б) 81 – 45,34 + 19,6 + 21,75; г) 81,9 : 4,5 : 0,28 • 1,2. - Запишите в виде выражения:
а) сумму числа х и произведения чисел а и b;
б) частное от деления числа а на разность чисел b и с;
в) произведение суммы чисел х и а и разности чисел х и b.
Контрольные вопросы и задания
- Приведите пример числового выражения и выражения с переменными.
2. Имеет ли смысл выражение: 36/(2 • 16 – 32) : (42 – 6 • 7)/(37 – 11) ?
3. Сравните значения выражений х + 3 и 3х при х = –4; 1,5; 5.
4. Приведите пример двойного неравенства и прочитайте его.
5. Как читаются знаки ≥ и ≤? Какое неравенство называется строгим и какое нестрогим? Приведите пример строгого неравенства, нестрогого неравенства.
Дополнительные упражнения к параграфу 1
Вы смотрели ознакомительную версию с цитатами из учебника: Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — М.: Просвещение. ГЛАВА I. Параграф 1. ВЫРАЖЕНИЯ. Цитаты из учебника использованы в учебных целях.


