Ознакомительная версия с цитатами из учебника для принятия решения о покупке. Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — М.: Просвещение (2020). ГЛАВА I учебника. § 4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ. (9. Среднее арифметическое, размах и мода. 10. Медиана как статистическая характеристика. 11. Формулы. Упражнения №№ 167 — 205. Контрольные вопросы и задания. Дополнительные упражнения №№ 253 — 257 к параграфу 4).
§ 4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
9. Среднее арифметическое, размах и мода
При изучении учебной нагрузки учащихся выделили группу из 12 семиклассников. Их попросили отметить в определённый день время (в минутах), затраченное на выполнение домашнего задания по алгебре. Получили такие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.
Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания по алгебре. Для этого надо сложить указанные 12 чисел и сумму разделить на 12:
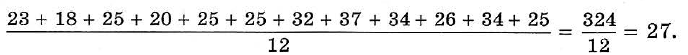
Число 27, полученное в результате, называют средним арифметическим рассматриваемого ряда чисел.

Мы нашли, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем по 27 мин. Проводя аналогичные наблюдения за этой группой учащихся, можно проследить, какова была средняя затрата времени на выполнение домашнего задания по алгебре в течение недели, сравнить среднюю затрату времени на выполнение в какой–либо день домашних заданий по алгебре и русскому языку и т. п. Заметим, что для серьёзных выводов о загруженности учащихся домашними заданиями необходимо выделить для наблюдений значительно большую группу, чем 12 человек.
Среднее арифметическое представляет собой то значение величины, которое получается, когда сумма всех наблюдаемых значений мысленно распределяется поровну между единицами наблюдения. Например, вычислив среднее арифметическое удоев молока, полученных за сутки на ферме от всех коров, мы найдём тот удой, который получили бы на ферме в эти сутки от одной коровы, если бы все коровы давали одинаковое количество молока, т. е. найдём среднесуточный удой молока на ферме от одной коровы. Аналогично находят среднюю урожайность пшеницы с 1 га в районе, среднюю выработку рабочего бригады за смену и т. п.
Заметим, что иногда вычисление среднего арифметического не даёт полезной информации. Например, нецелесообразно использовать в качестве обобщающего показателя среднюю урожайность зерновых и бахчевых культур в фермерском хозяйстве, средний размер обуви, которую носят учащиеся школы.
В рассмотренном примере мы нашли, что в среднем учащиеся затратили на выполнение домашнего задания по алгебре по 27 мин. Однако анализ приведённого ряда данных показывает, что время, затраченное некоторыми учащимися, существенно отличается от 27 мин, т. е. от среднего арифметического. Наибольший расход равен 37 мин, а наименьший – 18 мин. Разность между наибольшим и наименьшим расходом времени составляет 19 мин. В этом случае говорят, что размах ряда равен 19.

Размах ряда находят, когда хотят определить, как велик разброс данных в ряду. Пусть, например, в течение суток отмечали каждый час температуру воздуха в городе. Для полученного ряда данных полезно не только вычислить среднее арифметическое, показывающее, какова среднесуточная температура, но и найти размах ряда, характеризующий колебание температуры воздуха в течение этих суток.
При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели. Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, т. е. какое число встречается в ряду данных чаще всего. Нетрудно заметить, что таким числом является число 25. Говорят, что число 25 – мода рассматриваемого ряда.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем. Например, в ряду чисел
47, 46, 50, 52, 47, 52, 49, 45, 43, 53, 53, 47, 52
две моды – это числа 47 и 52, так как каждое из них встречается в ряду по три раза, а остальные числа – менее трёх раз.
В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.
Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Например, если изучаются данные о размерах мужских сорочек, проданных в определённый день в универмаге, то удобно воспользоваться таким показателем, как мода, который характеризует размер, пользующийся наибольшим спросом. Среднее арифметическое в этом случае не даёт полезной информации. Мода является наиболее приемлемым показателем при выявлении расфасовки некоторого товара, которой отдают предпочтение покупатели, цены на товар данного вида, распространённой на рынке, и т. п.
Рассмотрим ещё пример. Пусть, проведя учёт деталей, изготовленных за смену рабочими одной бригады, получили такой ряд данных:
36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37, 39, 38, 38, 36, 39, 36.
Найдём для него среднее арифметическое, размах и моду. Для этого удобно предварительно составить из полученных данных упорядоченный ряд чисел, т. е. такой ряд, в котором каждое последующее число не меньше (или не больше) предыдущего. Получим
35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.
Вычислим среднее арифметическое:

Размах ряда равен 39 – 35 = 4. Мода данного ряда равна 36, так как число 36 чаще всего встречается в этом ряду.
Итак, средняя выработка рабочих за смену составляет примерно 37 деталей; различие в выработке рабочих не превосходит 4 деталей; типичной является выработка, равная 36 деталям.
Среднее арифметическое ряда чисел может не совпадать ни с одним из чисел ряда, а мода, если она существует, обязательно совпадает с двумя или более числами ряда. Кроме того, в отличие от среднего арифметического понятие «мода» относится не только к числовым данным. Например, проведя опрос учащихся, можно получить ряд данных, показывающих, каким видом спорта они предпочитают заниматься, какую из развлекательных телевизионных программ они считают наиболее интересной. Модой будут служить те ответы, которые встречаются чаще всего. Этим и объясняется само название «мода».
Такие характеристики, как среднее арифметическое, размах и мода, находят применение в статистике – науке, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и её регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и т. п. Результаты статистических исследований широко используются для практических и научных выводов.
Упражнения
10. Медиана как статистическая характеристика
Рассмотрим ещё одну статистическую характеристику. Начнём с примера. В таблице показан расход электроэнергии в январе жильцами девяти квартир:
| Номер квартиры | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Расход электроэнергии, кВт • ч | 85 | 64 | 78 | 93 | 72 | 91 | 72 | 75 | 82 |
Составим из данных, приведённых в таблице, упорядоченный ряд: 64, 72, 72, 75, 78, 82, 85, 91, 93.
В полученном упорядоченном ряду девять чисел. Нетрудно заметить, что в середине ряда расположено число 78: слева от него записано четыре числа и справа четыре числа.
Говорят, что число 78 является срединным числом, или, иначе, медианой, рассматриваемого упорядоченного ряда чисел (от латинского слова mediana, которое означает «среднее»). Это число считают также медианой исходного ряда данных.
Приведём теперь другой пример. Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам добавили ещё десятую. Получили такую таблицу:
| Номер квартиры | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Расход электроэнергии, кВт • ч | 85 | 64 | 78 | 93 | 72 | 91 | 72 | 75 | 82 | 83 |
Так же как в первом случае, представим полученные данные в виде упорядоченного ряда чисел: 64, 72, 72, 75, 78, 82, 83, 85, 91, 93.
В этом числовом ряду чётное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдём среднее арифметическое этих чисел: (78 + 82)/2 = 80. Число 80, не являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы – слева от него находятся пять членов ряда и справа тоже пять членов ряда: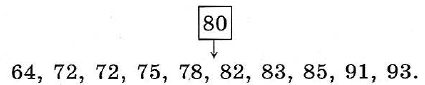
Говорят, что медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.

Если в упорядоченном числовом ряду содержится 2n – 1 членов, то медианой ряда является n–й член, так как n – 1 членов стоит до n–го члена и n – 1 членов – после n–го члена. Если в упорядоченном числовом ряду содержится 2n членов, то медианой является среднее арифметическое членов, стоящих на n–м и n + 1–м местах.
В каждом из рассмотренных выше примеров, определив медиану, мы можем указать номера квартир, для которых расход электроэнергии жильцами превосходит срединное значение, т. е. медиану.
Рассмотрим ещё пример. Известно, что 34 сотрудника отдела приобрели акции некоторого акционерного общества. Данные о числе акций, приобретённых сотрудниками, представлены в виде следующего упорядоченного ряда: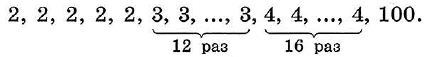
Найдём медиану этого ряда. Так как всего в ряду 34 числа, то медиана равна среднему арифметическому 17–го и 18–го членов, т. е. равна (3 + 4)/2 = 3,5.
Вычисляя среднее арифметическое этого ряда, найдём, что оно приближённо равно 6,2, т. е. в среднем сотрудники отдела приобрели примерно по б акций.
Мы видим, что в данном случае медиана лучше отражает реальную ситуацию, так как половину всех сотрудников составляют те, которые приобрели не более 3 акций.
Вообще среднее арифметическое зависит от значений всех членов в упорядоченном ряду данных, в том числе и от значений крайних членов, которые часто бывают наименее характерными для рассматриваемой совокупности данных. Поэтому при анализе данных сведения о среднем арифметическом часто дополняются указанием медианы.
Такие показатели, как среднее арифметическое, мода и медиана, по–разному характеризуют данные, полученные в результате наблюдений. Поэтому на практике при анализе данных в зависимости от конкретной ситуации используют какой–либо из этих показателей, либо два из них, либо даже все три.
Упражнения
Контрольные вопросы и задания
- Что называется средним арифметическим ряда чисел? Может ли среднее арифметическое ряда чисел не совпадать ни с одним из чисел ряда?
- Что называется размахом ряда чисел?
- Что называется модой ряда чисел? Любой ли ряд чисел имеет моду? Может ли ряд чисел иметь более одной моды? Может ли мода ряда чисел не совпадать ни с одним из чисел ряда?
- Что называется медианой ряда чисел? Может ли медиана ряда чисел не совпадать ни с одним из чисел ряда? Какое число является медианой упорядоченного ряда, содержащего 2n – 1 чисел? 2n чисел?
Дополнительные упражнения к параграфу 4

Вы смотрели ознакомительную версию с цитатами из учебника: Алгебра. 7 класс. Учебник / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др.; под ред. С.А. Теляковского — М.: Просвещение (2020). ГЛАВА I. § 4. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ. (9. Среднее арифметическое, размах и мода. 10. Медиана как статистическая характеристика. Для тех, кто хочет знать больше. 11. Формулы. Упражнения №№ 167 — 205. Контрольные вопросы и задания. Дополнительные упражнения №№ 253 — 257 к параграфу 4).





