Онлайн. Глава 1. Линейное уравнение с одной переменной. § 4. Решение задач с помощью графов. Упражнения №№ 4.1 — 4.14. Итоги главы 1. Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Алгебра 7 класс Мерзляк, Поляков (угл.изуч.)
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
§ 4. Решение задач с помощью графов.
Вы хорошо знаете, что составление уравнений — это не единственный способ решения текстовых задач. Также эффективным приёмом является «решение задач по действиям», т. е. арифметическим способом, когда в определённой последовательности находят значения числовых выражений и в конечном итоге получают ответ. Здесь переводом задачи из реальной жизни на математический язык является запись одного или нескольких числовых выражений.
Заметим, что в начальной школе именно с этого способа вы начали знакомство с методами решения текстовых задач.
Методы решения задач, представляющие реальные ситуации, разнообразны и далеко не исчерпываются моделями в виде числовых выражений или уравнений. Изучая математику, вы будете расширять список соответствующих моделей. Сейчас познакомимся с методом, применение которого основано на построении математической модели в виде геометрической фигуры. Заметим, что вы уже использовали элементы этого приёма, когда в задачах на движение строили различные схемы: движения в одном направлении, в противоположных направлениях, навстречу друг другу и т. п.
ПРИМЕР 1. В регионе есть пять городов. Можно ли эти города связать дорогами так, чтобы из каждого города выходили: 1) четыре дороги; 2) три дороги?
Решение. Построим схему, на которой города будут изображены точками А, В, С, D и Е. Дорогу, соединяющую два города, будем изображать в виде отрезка. Например, на рисунке 4.1 показана кольцевая схема дорог.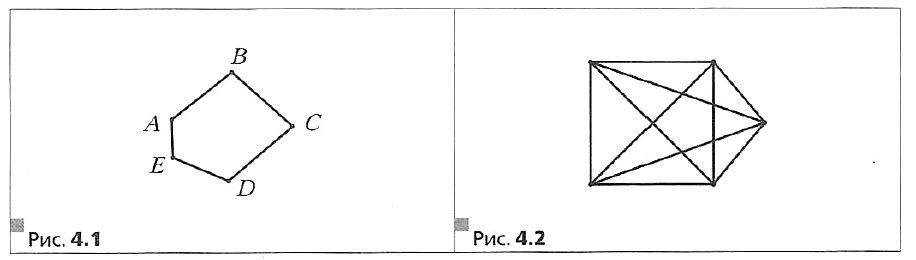
1) Задача сводится к тому, чтобы выяснить, можно ли пять точек плоскости соединить отрезками так, чтобы из каждой точки выходили четыре отрезка. На рисунке 4.2 показано, как это сделать.
2) Предположим, что такая схема возможна. Подсчитаем, сколько отрезков будет на этой схеме. Имеем: 5*3 = 15 (отрезков). Однако при таком подсчёте каждый отрезок был учтён дважды. Получается, что количество отрезков равно 15/2. Это число не является целым. Получили противоречие.
Ответ: 1) да; 2) нет. ■
В повседневной жизни нам нередко приходится пользоваться рисунками, состоящими из точек, некоторые из которых соединены линиями. Например, на рисунке 4.3 изображена схема метрополитена Санкт–Петербурга.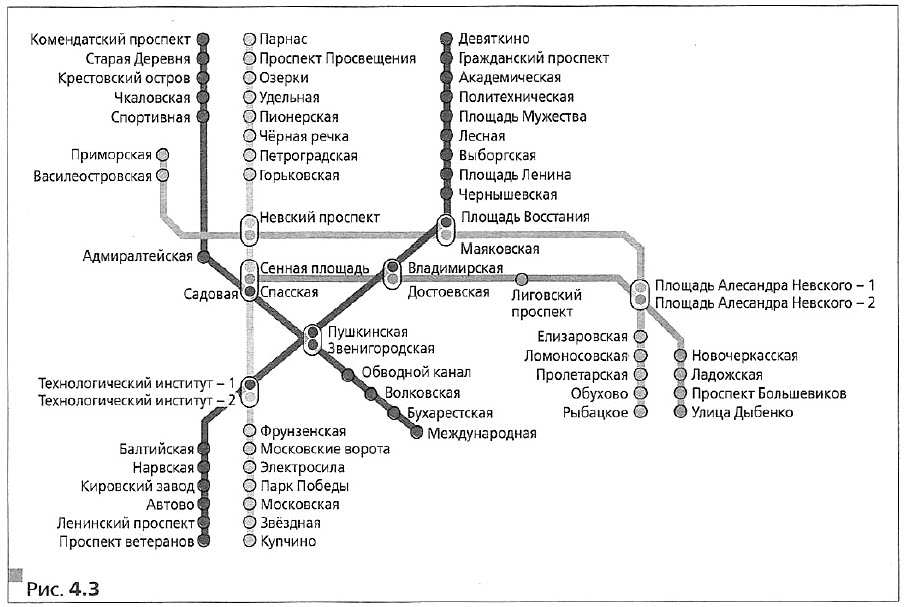
Такие рисунки называют графами. Точки на рисунке называют вершинами графа, а соединяющие их линии — рёбрами графа.
На рисунке 4.4 приведены ещё несколько примеров графов.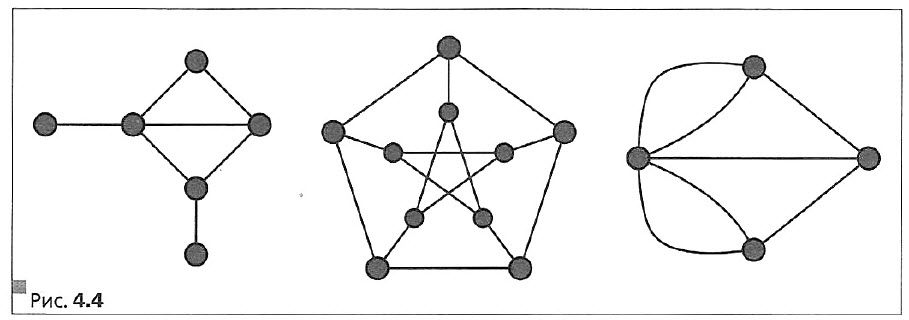
Вооружившись фантазией, можно представить, что эти рисунки иллюстрируют схемы автомобильных дорог, план городка аттракционов и даже отношения между людьми, например такие как дружба.
Любопытно, что рисунки такого вида и дворянский титул имеют одинаковое название — граф. Это слово произошло от латинского grafito — пишу.
Графами удобно пользоваться тогда, когда хотят описать связь между объектами, событиями или процессами. Проиллюстрируем сказанное на примере решения следующей задачи.
ПРИМЕР 2. Существует ли компания из 16 человек, в которой каждый дружит ровно с 6 другими людьми из этой компании?
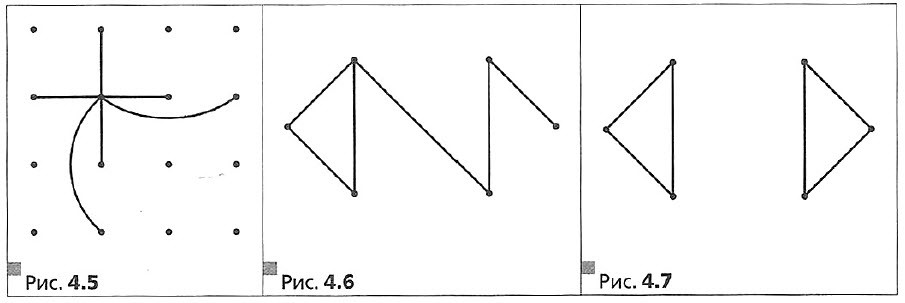
Решение. Нарисуем 16 точек так, как показано на рисунке 4.5. Эти точки изображают 16 человек данной компании. Возьмём произвольную точку и соединим её со всеми точками, находящимися с ней на одной горизонтали или вертикали. Получили 6 рёбер графа, которые соответствуют дружеским связям. Так можно поступить с каждой из 16 точек.
Ответ: существует. ■
Количество рёбер, выходящих из вершины графа, называют степенью этой вершины. Например, степень каждой вершины, изображённой на рисунке 4.1, равна 2.
Заметим, что решение задачи 2 из примера 1 свелось к выяснению вопроса: существует ли пятивершинный граф, степень каждой вершины которого равна 3? Ответ на этот вопрос оказался отрицательным. На самом деле имеет место более общий факт: в любом графе количество вершин, степень которых нечётная, является чётным числом. Он следует из того, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер, а следовательно, является чётным числом.
При проектировании системы транспортных маршрутов важнейшим требованием является возможность попасть из любого населённого пункта в любой другой. На языке теории графов это означает, что соответствующий граф должен обладать таким свойством: любые две вершины графа соединены некоторым путём, т. е. последовательностью рёбер, каждое следующее из которых начинается в конце предыдущего. Граф, обладающий описанным свойством, называют связным.
На рисунке 4.6 изображён связный граф, а граф, изображённый на рисунке 4.7, связным не является.
ПРИМЕР 3. В некотором регионе 9 городов. Из каждого города выходят 4 дороги, связывающие его с четырьмя городами этого региона. Докажите, что из любого города можно проехать в любой другой город.
Решение. Предположим, что не существует пути, соединяющего города А и В. Каждый их этих двух городов соединён с четырьмя другими (отличными от А и В).
Если город А и город В соединены с одним и тем же городом, это означает, что существует путь, соединяющий города А и В. Следовательно, чтобы такого пути не существовало, все 8 городов, с которыми соединены города А и В, должны быть различными. Добавив к ним города А и В, получаем, что количество городов в данном регионе не меньше 10, что противоречит условию задачи. Следовательно, наше предположение неверно. ■
Рассмотренный пример иллюстрирует следующий общий факт: если граф имеет n вершин и степень каждой вершины не меньше, чем (n — 1)/2, то такой граф является связным.
Воспользовавшись идеей решения задачи из примера 3, докажите этот факт самостоятельно.
ИТОГИ ГЛАВЫ 1.

Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 4. Решение задач с помощью графов.

