Геометрия ГДЗ Атанасян Учебник. Задания 333 — 350. Решебник практических заданий и задач из учебника «Геометрия 7 класс» УМК Атанасян, Бутузов и др. Задачи повышенной трудности к главам III и IV. Ответы на задания и задачи представлены для родителей в конце статьи.
Геометрия (Атанасян) Учебник
Задачи повышенной трудности к главам III и IV
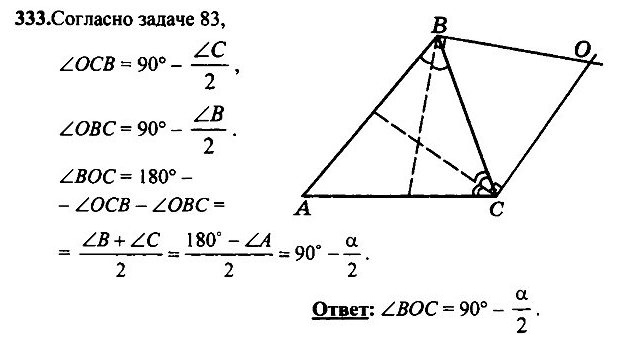
- Прямые, содержащие биссектрисы внешних углов при вершинах В и С треугольника АВС, пересекаются в точке О. Найдите угол ВОС, если угол А равен α.
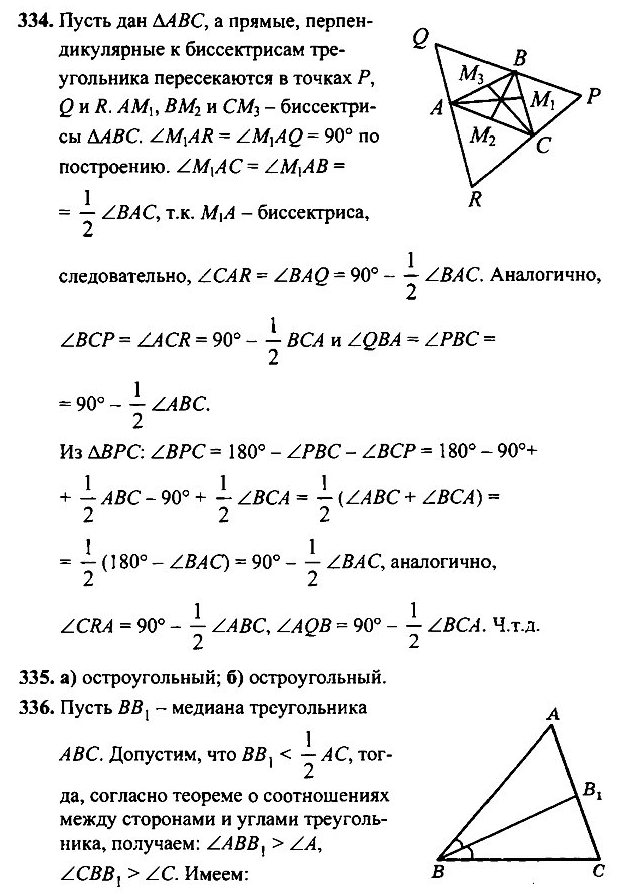
- Через каждую вершину данного треугольника проведена прямая, перпендикулярная к биссектрисе треугольника, исходящей из этой вершины. Отрезки этих прямых вместе со сторонами данного треугольника образуют три треугольника. Докажите, что углы этих треугольников соответственно равны.
- В каждом из следующих случаев определите вид треугольника: а) сумма любых двух углов больше 90°; б) каждый угол меньше суммы двух других углов.
- Докажите, что угол треугольника является острым, прямым или тупым, если медиана, проведённая из вершины этого угла, соответственно больше, равна или меньше половины противоположной стороны.
- Внутри равнобедренного треугольника АВС с основанием ВС взята такая точка М, что ∠MBC = 30°, ∠MCB= 10°. Найдите угол АМС, если ∠BAC = 80°.
- Докажите, что любой отрезок с концами на разных сторонах треугольника не больше наибольшей из сторон треугольника.
- Отрезок ВВ1 — биссектриса треугольника АВС. Докажите, что ВА > В1А и ВС > В1С.
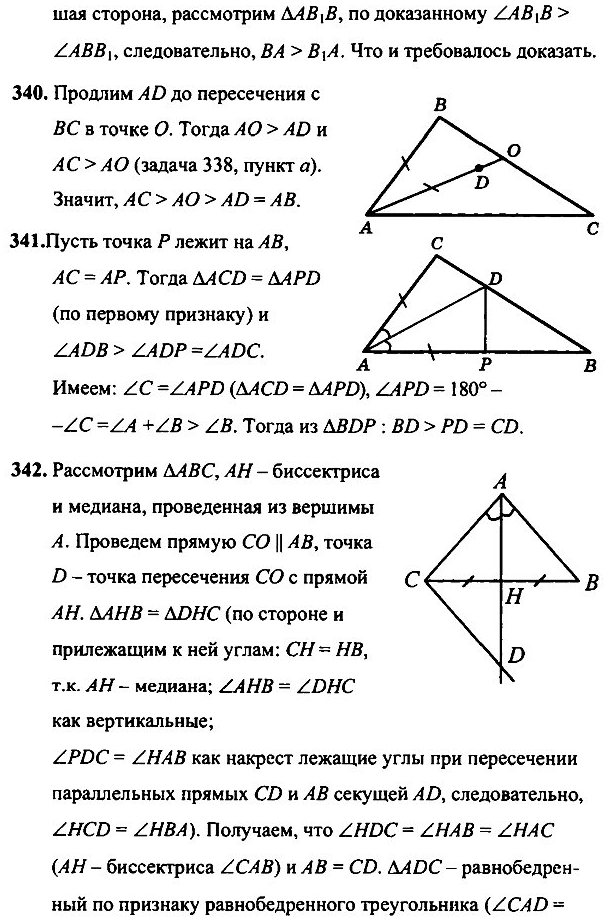
- Внутри треугольника АВС взята такая точка D, что AD = AB. Докажите, что АС > АВ.
- В треугольнике АВС сторона АВ больше стороны АС, отрезок AD — биссектриса. Докажите, что ∠ADB > ∠ADC и BD > CD.
- Докажите теорему: если в треугольнике биссектриса является медианой, то треугольник равнобедренный.
- Две стороны треугольника не равны друг другу. Докажите, что медиана, проведённая из их общей вершины, составляет с меньшей из сторон больший угол.
- В треугольнике АВС стороны АВ и АС не равны, отрезок AM соединяет вершину А с произвольной точкой М стороны ВС. Докажите, что треугольники АМВ и АМС не равны друг другу.
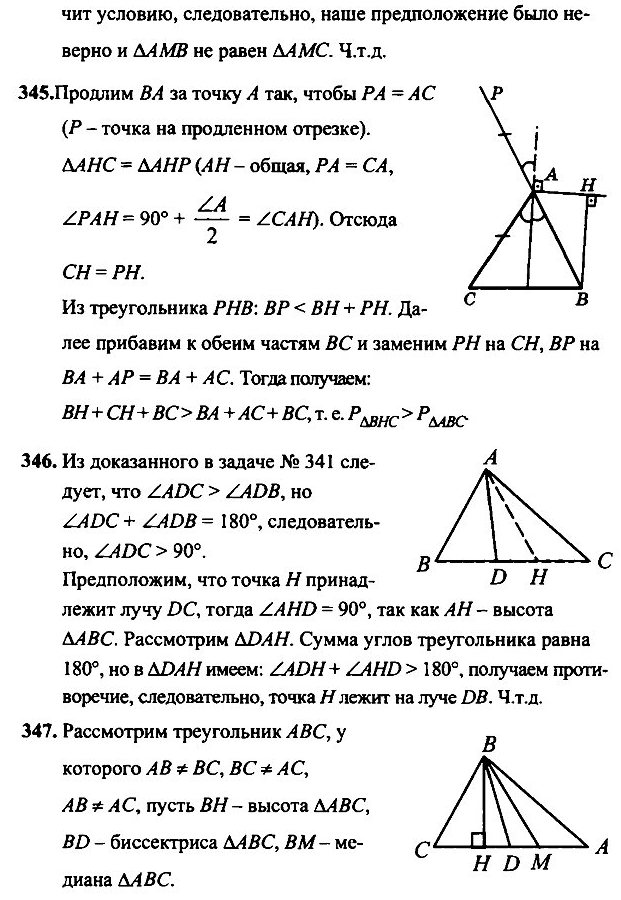
- Через вершину А треугольника АВС проведена прямая, перпендикулярная к биссектрисе угла А, а из вершины В проведён перпендикуляр ВН к этой прямой. Докажите, что периметр треугольника ВСН больше периметра треугольника АВС.
- В треугольнике АВС, где АВ < АС, отрезок AD — биссектриса, отрезок АН — высота. Докажите, что точка Н лежит на луче DB.
- Докажите, что в неравнобедренном треугольнике основание биссектрисы треугольника лежит между основаниями медианы и высоты, проведённых из этой же вершины.
- Докажите, что в прямоугольном треугольнике с неравными катетами биссектриса прямого угла делит угол между высотой и медианой, проведёнными из той же вершины, пополам.
- Медиана и высота треугольника, проведённые из одной вершины угла треугольника, делят этот угол на три равные части. Докажите, что треугольник прямоугольный.
- В треугольнике АВС высота ААХ не меньше стороны ВС, а высота ВВХ не меньше стороны АС. Докажите, что треугольник АВС — равнобедренный и прямоугольный.
ОТВЕТЫ на задания 333 — 350:
Вы смотрели: ГДЗ Атанасян Учебник. Задания 333 — 350. Решебник практических заданий и задач из учебника «Геометрия 7 класс» УМК Атанасян, Бутузов и др. Задачи повышенной трудности к главам III и IV. Ответы на задания и задачи.
Вернуться к Списку заданий учебника по Геометрии 7 класс Атанасян.