ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович (2019). Глава 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 40. Разложение многочленов на множители с помощью комбинации различных приёмов. ОТВЕТЫ на упражнения 40.1 — 40.30). Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 Мордкович (упр. 40.1 — 40.30)
§ 40. Разложение многочленов на множители с помощью комбинации различных приёмов
Нажмите на спойлер, чтобы посмотреть ответ на задание:
Разложите многочлен на множители:
Задание № 40.1. a) 5х2 – 5; б) 18b2 – 2с2; в) 3а2 – 12; г) 10x2 – 10y2.
Задание № 40.2. а) x3 – 81х; б) 3у3 – 300y; в) 64а – а3; г) 2b3 – 288b.
Задание № 40.3. a) с3 – 0,25с; б) 50m3 – 2n2m; в) 0,04s – sa2; г) 48р2q – 75q3.
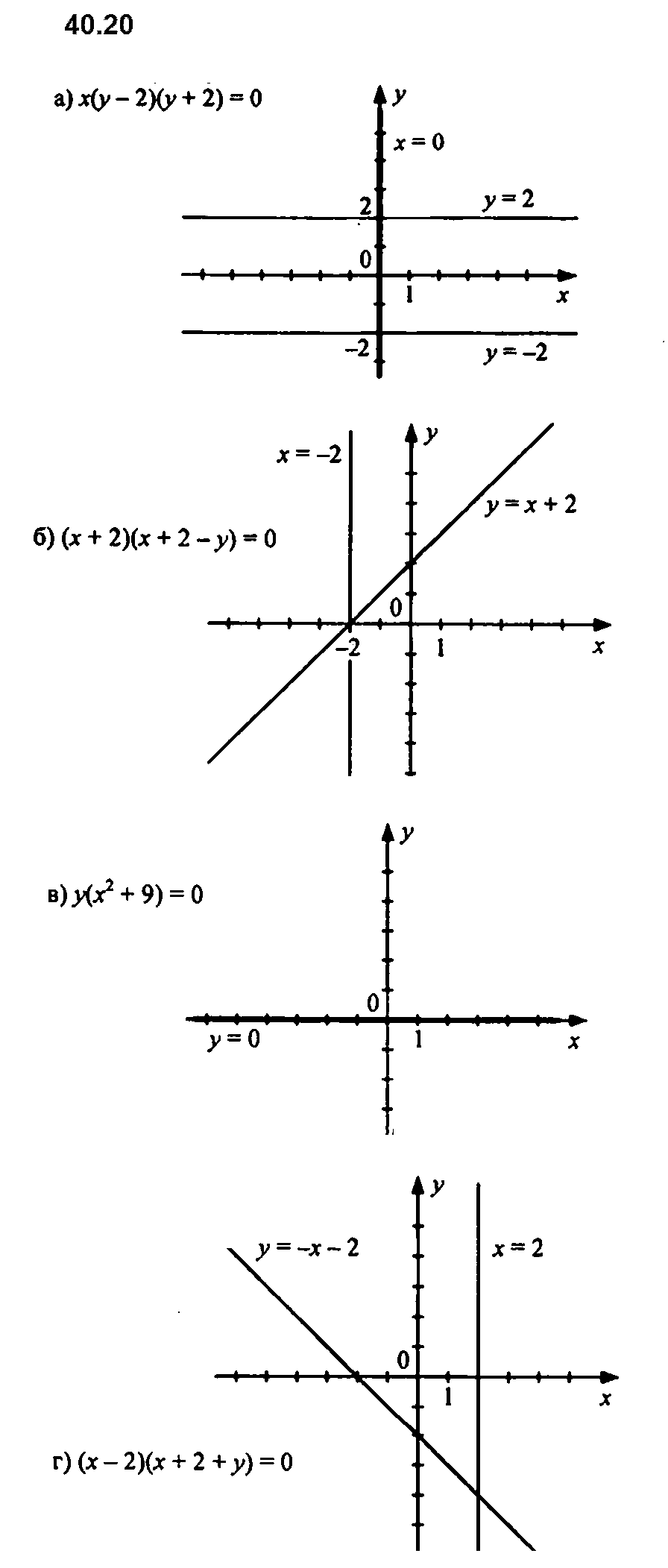
Задание № 40.20. Постройте график уравнения:
а) ху2 = 4х; б) х2 + 4х – ху – 2у + 4 = 0; в) ух2 + 9у = 0; г) х2 + ху – 2у – 4 = 0.
Разложите многочлен на множители, используя метод выделения полного квадрата двучлена:
Задание № 40.21. а) х2 – 10х + 24; б) у4 – 14у2 + 40; в) b4+ 4b2 – 5; г) а2 – 6а + 5.
Задание № 40.22. а) 4а2 – 12аb + 5b2; б) 9с2 – 24cd + 7d2; в) 25а2 – 20аb – 12b2; г) 9m2 – 30mk + 16k2.
Разложите многочлен на множители, представив один из членов многочлена в виде суммы подобных слагаемых:
Задание № 40.23. а) а2 + 7а + 10; б) х4 + 7х2 + 12; в) b2 – 3b – 4; г) у4 – 5у2 + 4.
Задание № 40.24. а) х2 + 5ху + 6у2; б) 4m2 – 5mn + n2; в) p2 – pq – 2q2; г) а2 + 7аb + 6b2.
Решите уравнение:
Задание № 40.25. а) x3 – х = 0; б) 16у – у3 = 0; в) с3 + с2 = 0; г) d3 + d = 0.
Задание № 40.26. а) x3 + х2 – 4х – 4 = 0; б) у3 + 2у2 – 4у – 8 = 0; в) 9z + 9 – z3 – z2 = 0; г) p3 – p2 – 4р + 4 = 0.
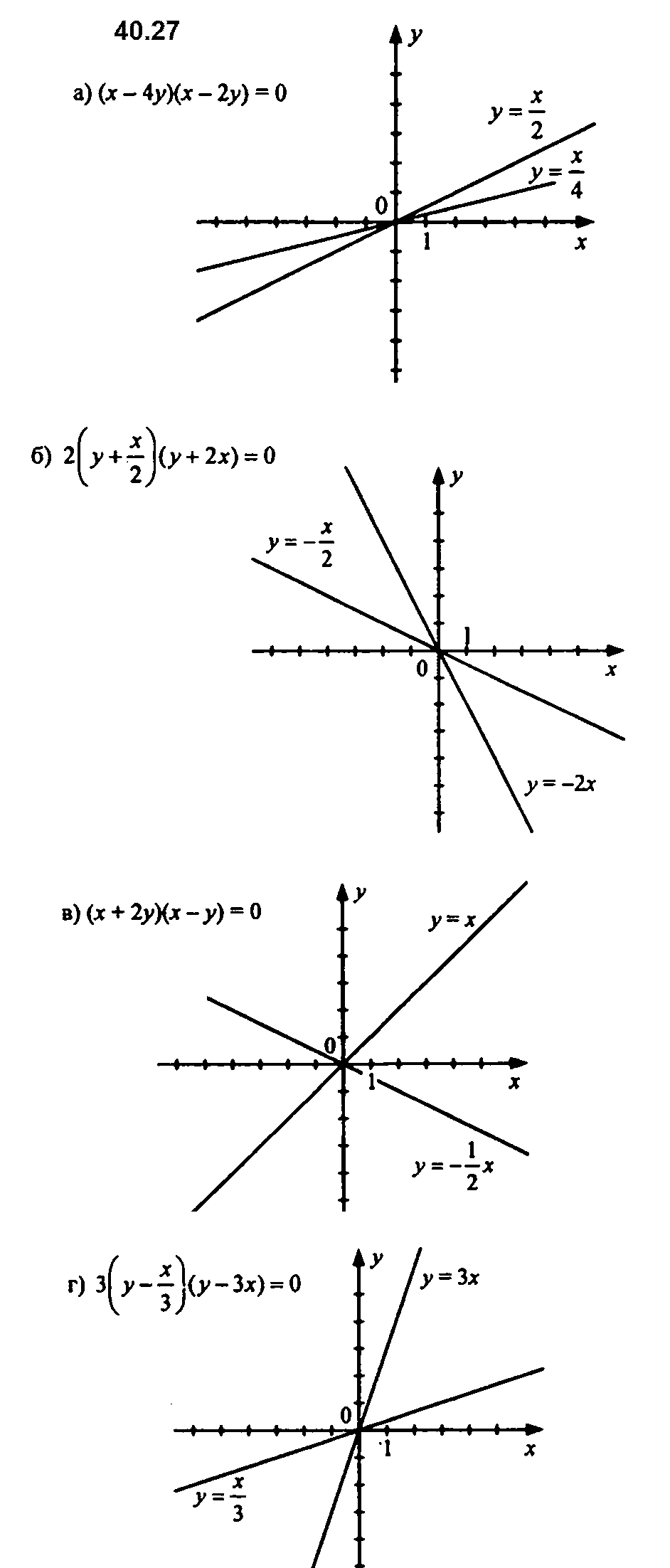
Задание № 40.27. Постройте график уравнения:
а) х2 – 6ху + 8у2 = 0; б) 2х2 + 5ху + 2у2 = 0; в) х2 + ху – 2у2 = 0; г) 3х2 – 10хy + 3у2 = 0.
Задание № 40.28. Пусть x1 + х2 = 7, х1х2 = 2. Вычислите:
а) х1х22 + х12х2; б) х12 + х1х2 + х22; в) х12 + х22; r) x13 + х23.
Задание № 40.29. Пусть x1 + х2= 5, x1х2 = –3. Вычислите:
а) х14 + х24; б) (x1 – х2)2; в) x13x22 + x12x23; г) x12х24 + х14х22.
Задание № 40.30. Решите уравнение:
а) х2 – 5х + 6 = 0; б) х2 – 5х – 6 = 0; в) х2 + 5х + 6 = 0; г) х2 + 5х – 6 = 0.
Решение № 40.30.
а) х2 – 5х + 6 = 0 или х^2–5х+6=0
х2 – 5х + 6 = х • х – 2х – 3х + 6 = х(х – 2) – 3(х – 2) = (х – 3)(х – 2) = 0
х – 3 = 0 и х – 2 = 0
Ответ: x1 = 2, x2 = 3.
б) х2 – 5х – 6 = 0 или х^2–5х–6=0
х2 – 5х – 6 = х • х + х – 6х – 6 = х(х + 1) – 6(х + 1) = (х – 6)(х + 1) = 0
х – 6 = 0 и х + 1 = 0
Ответ: x1 = 6, x2 = –1.
в) х2 + 5х + 6 = 0 или х^2+5х+6=0
х2 + 5х + 6 = х • х + 2х + 3х + 6 = х(х + 2) + 3(х + 2) = (х + 3)(х + 2) = 0
х + 3 = 0 и х + 2 = 0
Ответ: x1 = –2, x2 = –3.
г) х2 + 5х – 6 = 0 или х^2+5х–6=0.
х2 + 5х – 6 = х • х + 6х – х – 6 = х(х + 1) – (х + 1) = (х + 6)(х – 1) = 0
х + 6 = 0 и х – 1 = 0
Ответ: x1 = 1, x2 = –6.
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 7. Разложение многочленов на множители. § 40. Разложение многочленов на множители с помощью комбинации различных приёмов. ОТВЕТЫ на упражнения 40.1 — 40.30.
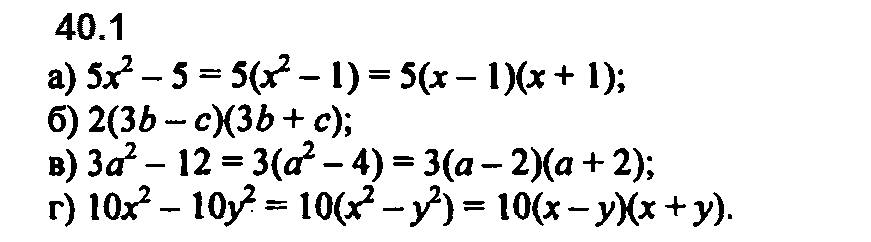
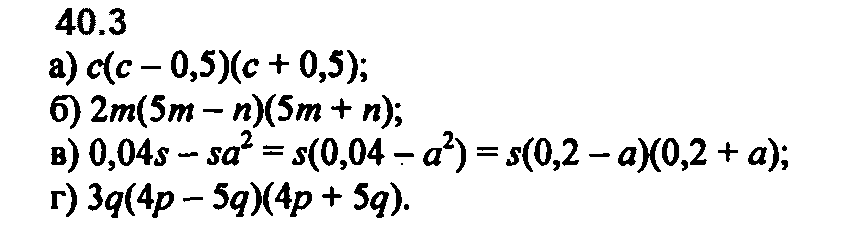
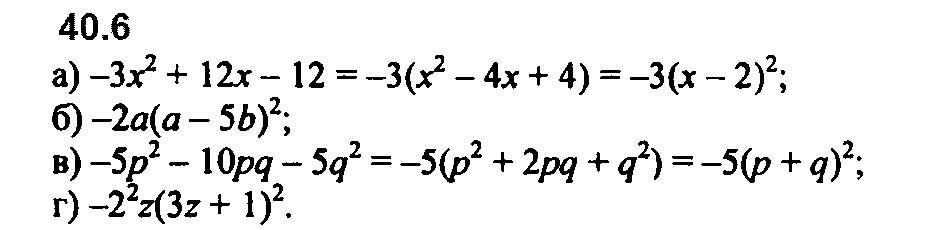
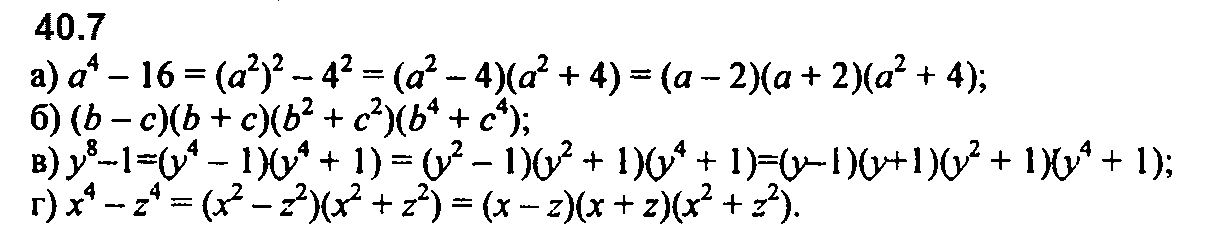
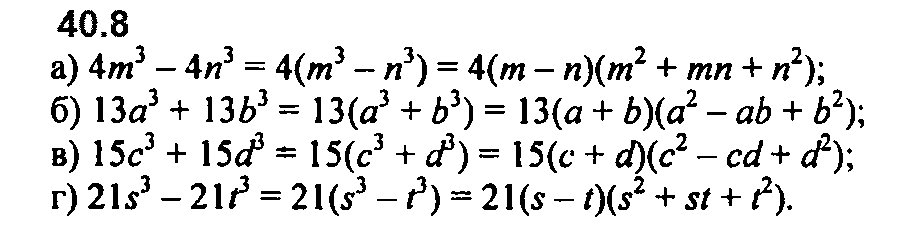
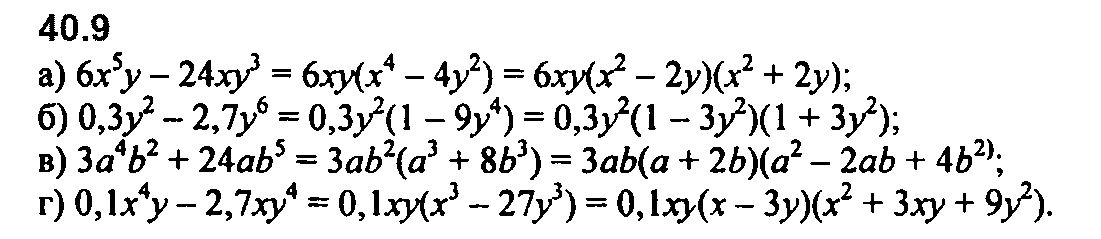
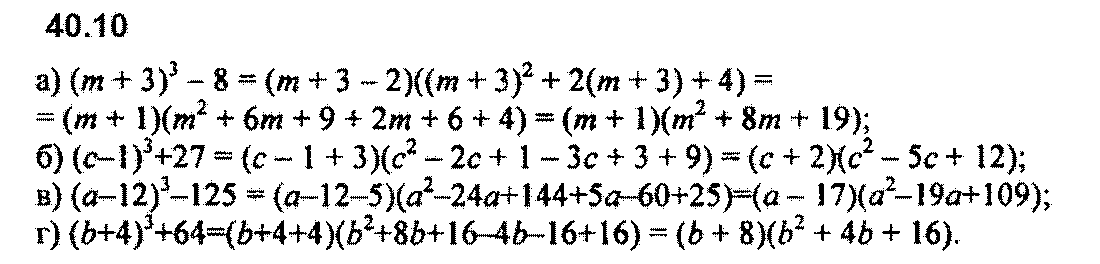
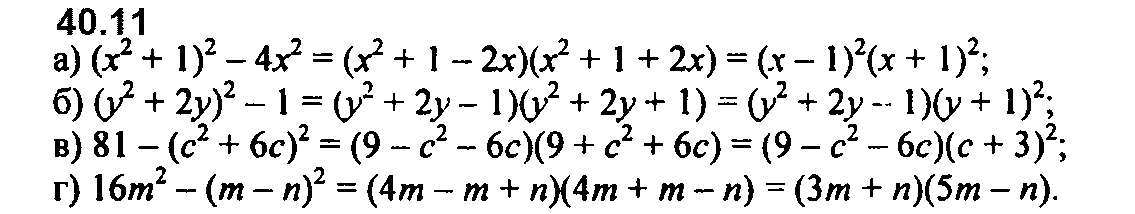
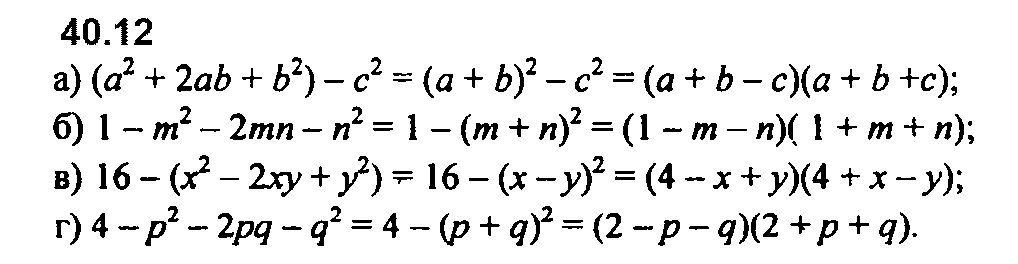
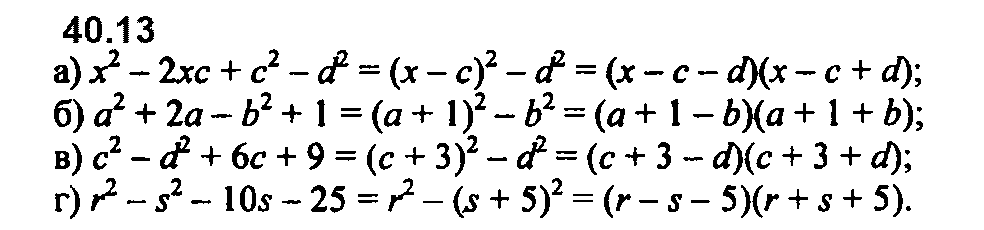
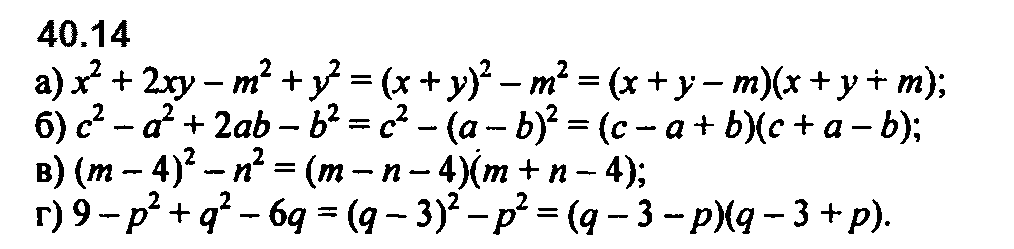
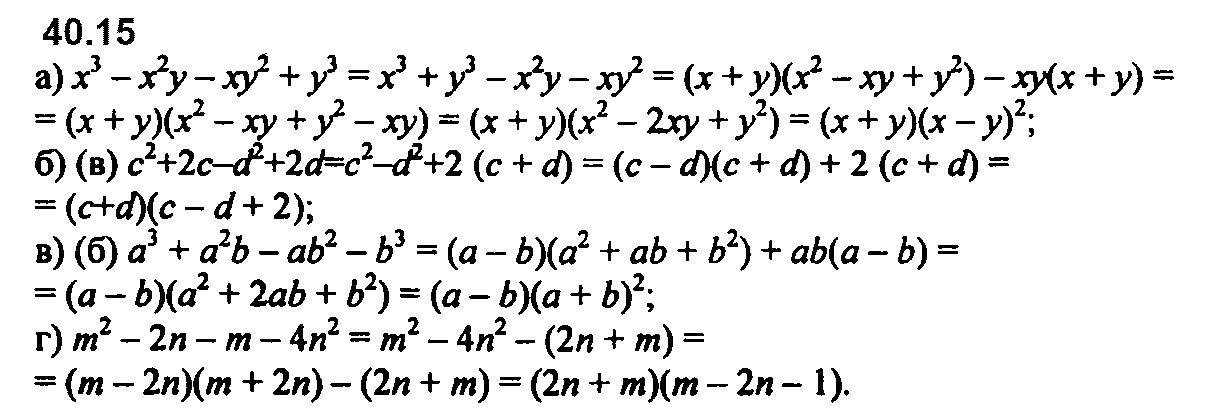
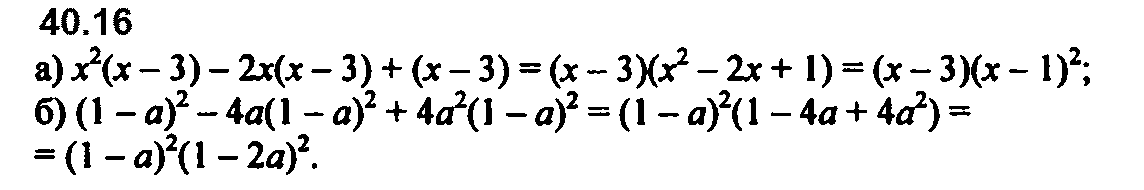
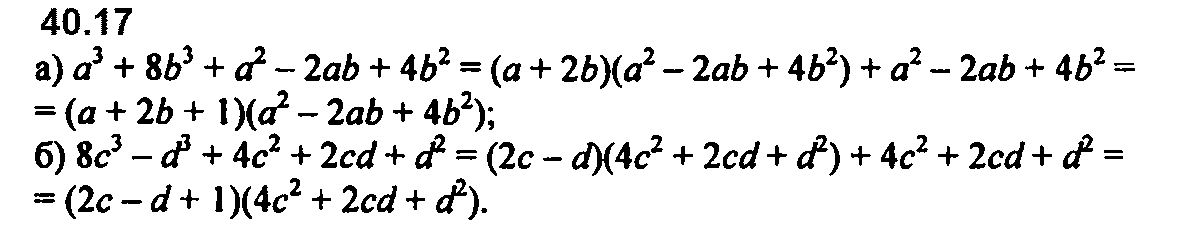
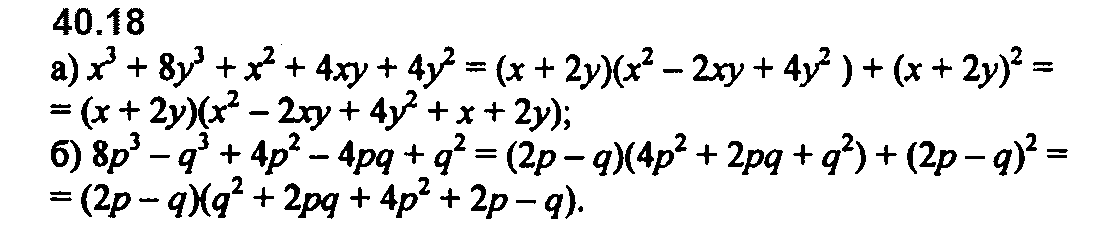
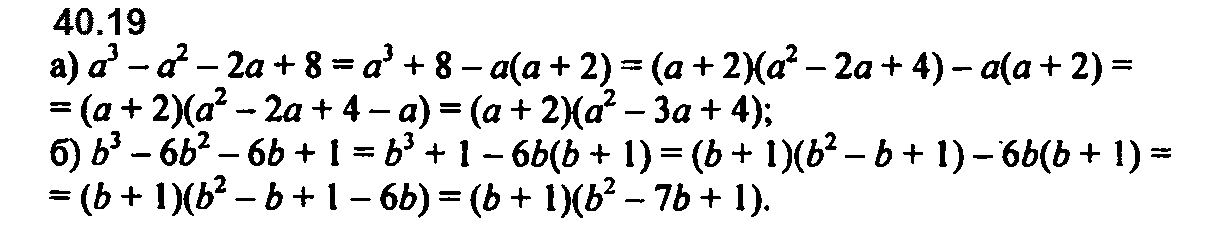
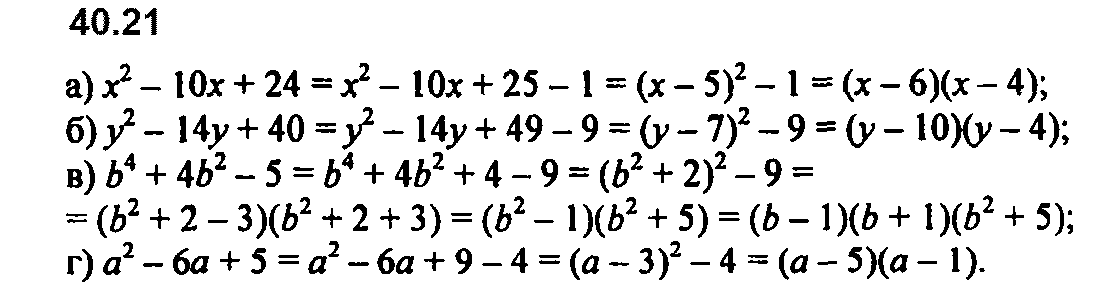
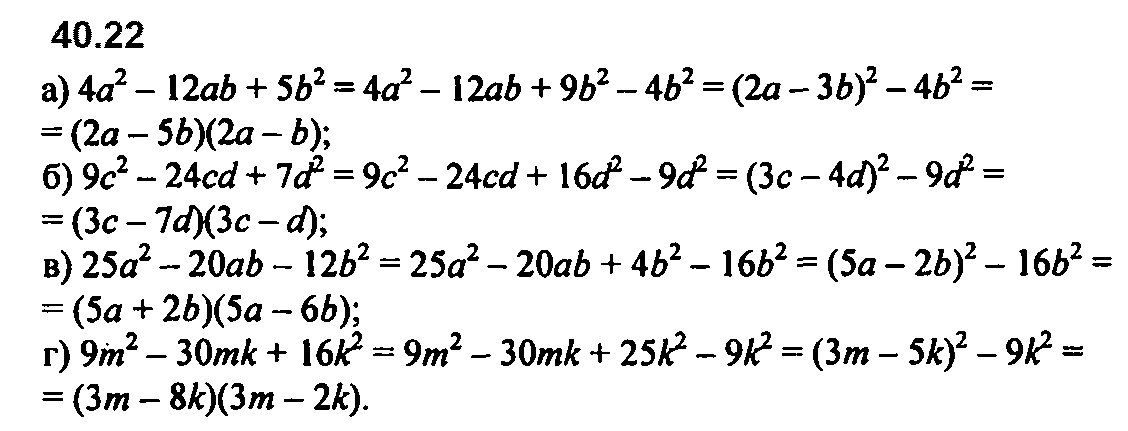
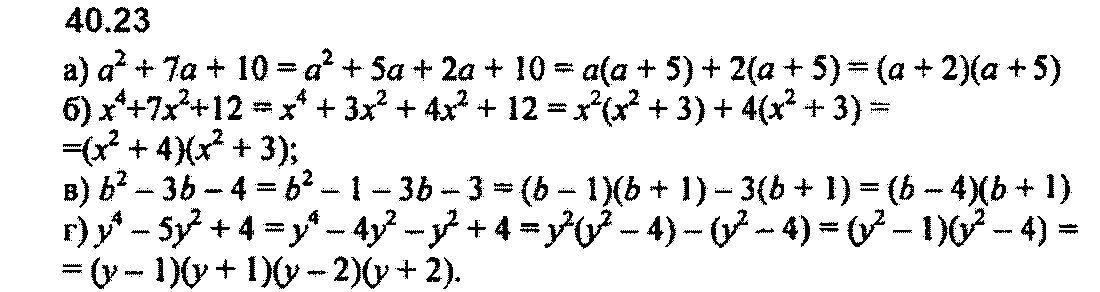
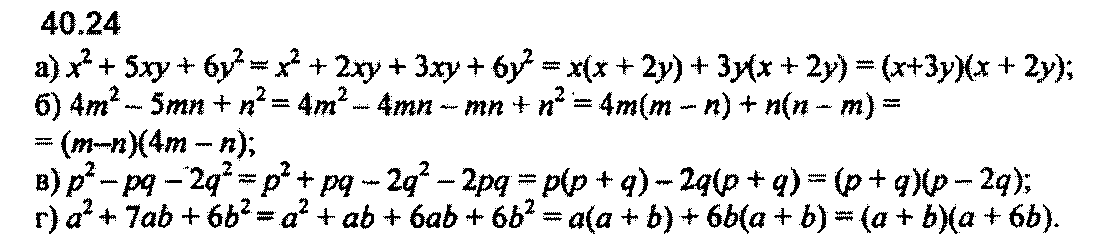
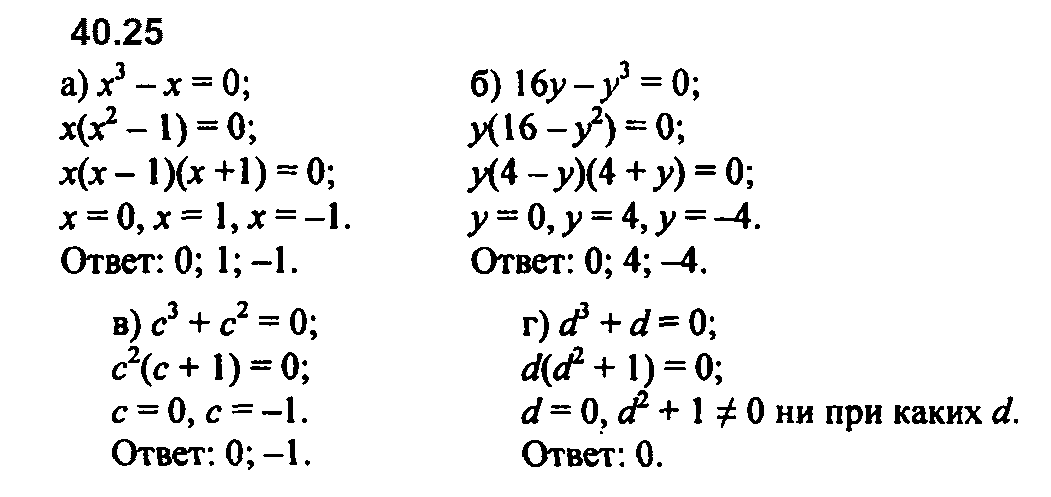
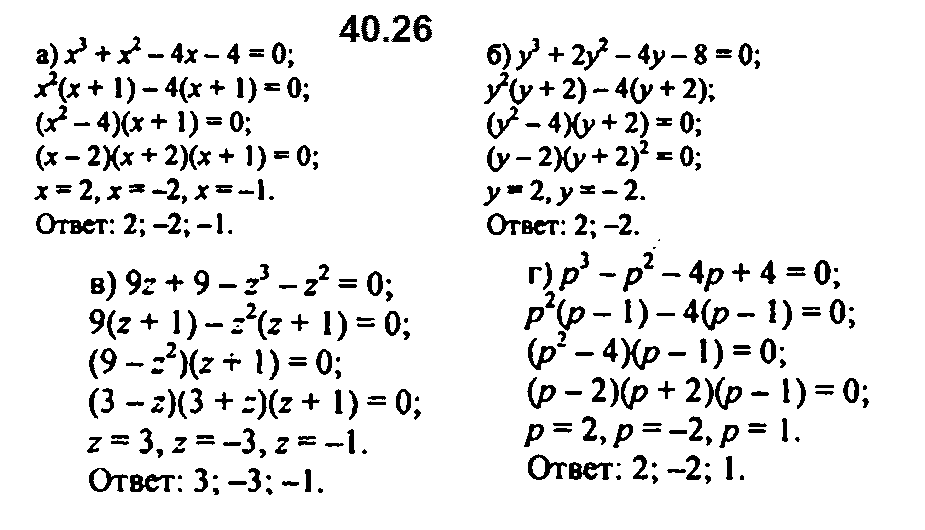
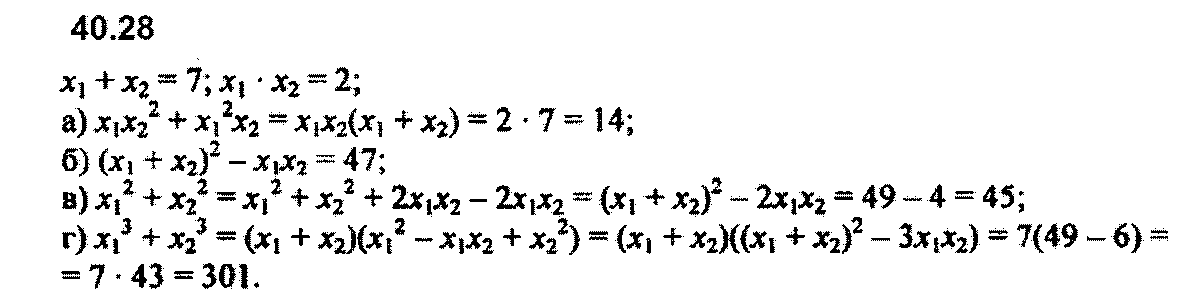
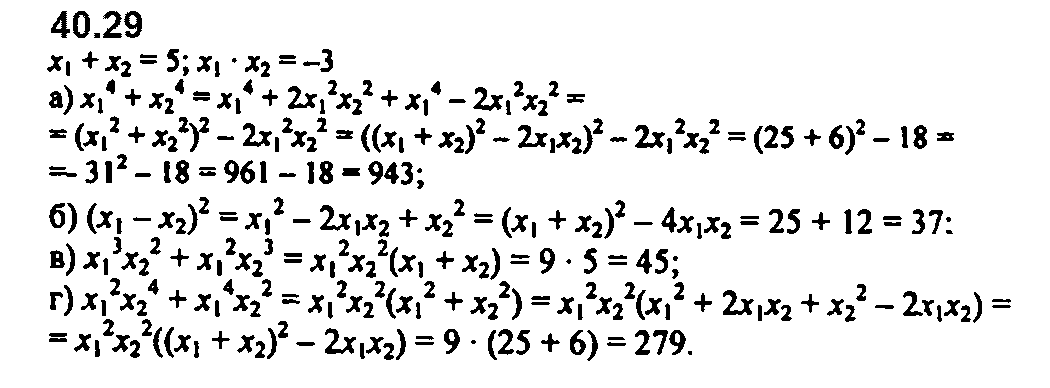
Номер 40.12 б и в перепутаны местами.
исправлено!
Почему у вас не во всех примерах подробное (полное) решение я сейчас нахожусь на 40.2(б) и там нету решения там просто ответ
Исправлено
Нет задания 40.30
Добавили решение на 40.30.