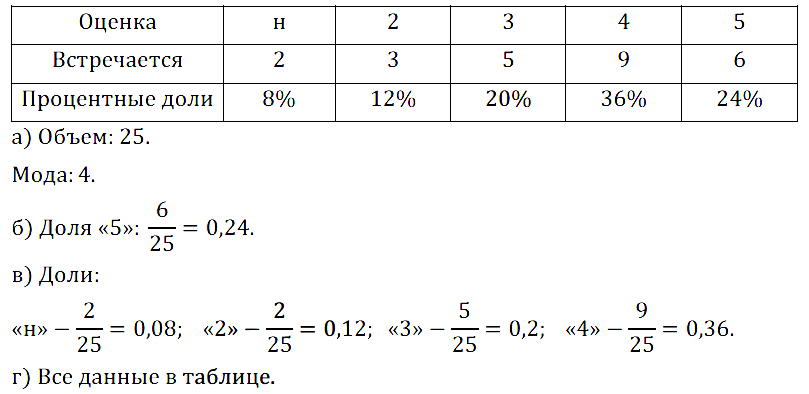ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2020). Глава 2. Линейная функция. § 12. Упорядочение данных, таблицы распределения. (ответы на упражнения 12.1 — 12.6). Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 Мордкович (упр. 12.1 — 12.6)
§ 12. Упорядочение данных, таблицы распределения
№ 12.1. Возьмите таблицу, составленную в примере 2 §12 учебника:
а) найдите объём и моду оценок (включая «н») за контрольную;
б) определите часть (долю) пятёрок среди всех оценок (включая «н»);
в) определите части (доли) остальных оценок;
г) составьте таблицу распределения процентных долей оценок.
№ 12.2. Приведите левые части следующих уравнений к виду ах + by + с:
1) 3х – 4у + 5 = 0; 8) 5 – 1,5(у – 2х) = 0;
2) 0,5(4х + 1) – у = 0; 9) 2(х + 2у) – 21 = 0;
3) у – х — 0; 10) –(2у – 3х) + 1 = 0;
4) х = 0; 11) 5 – 3(у – х) = 0;
5) у = 0; 12) –(х – у) + 1 = 0;
6) 5у – 4 = 0; 13) 0,5(3у – 2х) + 5 = 0.
7) 3(х + 2у) – 8 = 0;
а) Запишите ряд данных, состоящий из коэффициентов при переменной х.
б) Найдите объём и размах полученного ряда данных.
в) Составьте упорядоченный ряд данных и найдите его медиану.
г) Чему равна мода? Сколько раз она встретилась в ряде данных?
д) Сколько раз встретилось число –1, число 0, число 1, число 2?
е) Составьте таблицу распределения полученных данных.
ж) Сложите все числа во второй строке таблицы распределения. Объясните, почему ответ совпал с объёмом ряда данных.
з) Может ли во второй строке какой–либо таблицы распределения данных стоять число О?
Десять спортсменов соревновались в прыжках в высоту, в длину, вправо и влево. Вот какие места они заняли: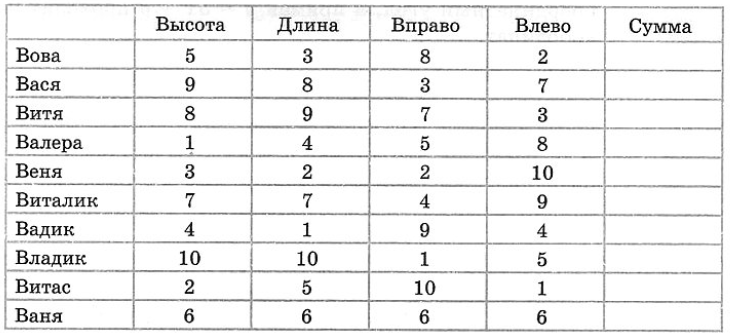
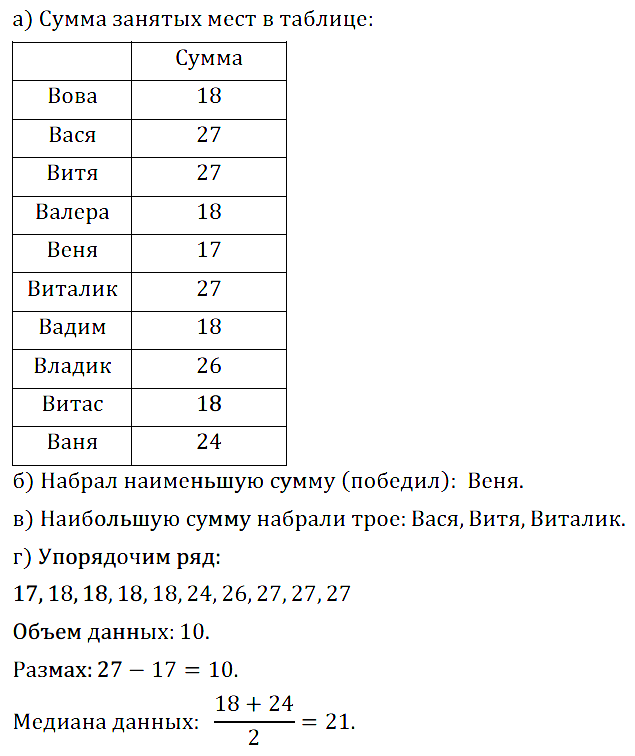
№ 12.3. а) Для каждого прыгуна подсчитайте сумму занятых им мест.
б) Кто из прыгунов победил (набрал наименьшую сумму мест)?
в) Кто из прыгунов оказался последним (набрал наибольшую сумму мест)?
г) Каковы объём, размах и медиана ряда данных, состоящих из суммы занятых мест?
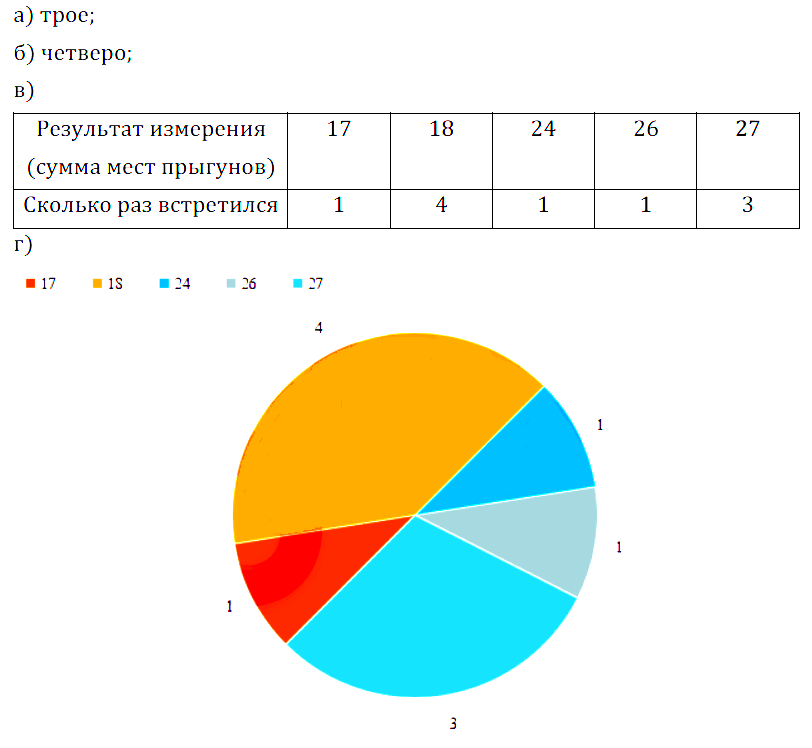
№ 12.4. а) Сколько прыгунов набрали 27 в сумме мест?
б) Сколько прыгунов набрали 18 в сумме мест?
в) Составьте таблицу распределения сумм мест.
г) Постройте круговую диаграмму распределения сумм мест.
Используя в качестве коэффициентов k и m числа –2, –1, 0, 1, 2, составляют различные формулы линейной функции у = kx + m.
№ 12.5 а) Сколько всего различных формул можно составить?
б) У скольких из полученных формул коэффициент k будет отрицателен?
в) У скольких из этих формул коэффициент m будет неотрицателен?
г) У скольких из этих формул коэффициенты k и m будут различны по знаку?
№ 12.6. Графики скольких из этих функций будут:
а) проходить через начало координат;
б) проходить через точку А(1; 0);
в) проходить через точку В(0; 1);
г) параллельны графику функции у = 5 – х ?
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина). Глава 2. Линейная функция. § 12. Упорядочение данных, таблицы распределения (ответы на упражнения 12.1 — 12.6).