Практические задания и задачи №№ 100-120 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 2. Медианы, биссектрисы и высоты треугольника. (16. Перпендикуляр к прямой. 17. Медианы, биссектрисы и высоты треугольника. 18. Свойства равнобедренного треугольника). Геометрия Атанасян Задачи 100-120 + Ответы.
◄ Задачи 87-99 ОГЛАВЛЕНИЕ учебника Задачи 121-142 ►
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Геометрия 7 класс (УМК Атанасян)
Практические задания
и задачи №№ 100-120
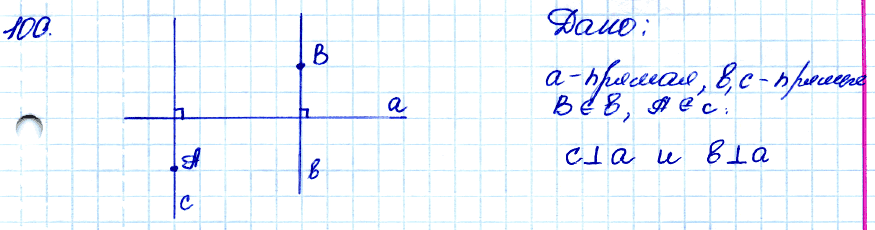
№ 100. Начертите прямую а и отметьте точки А и В, лежащие по разные стороны от прямой а. С помощью чертёжного угольника проведите из этих точек перпендикуляры к прямой а.
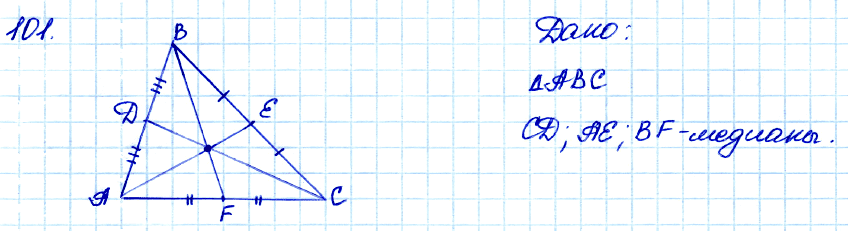
№ 101. □ Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите медианы треугольника.
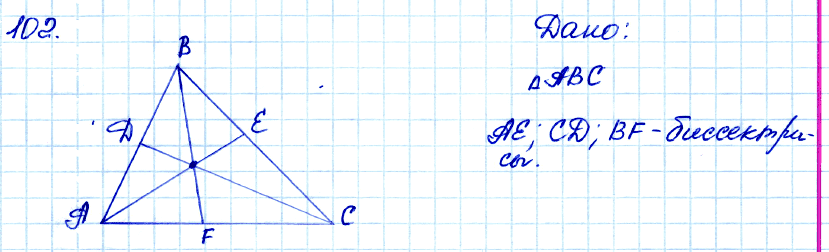
№ 102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.
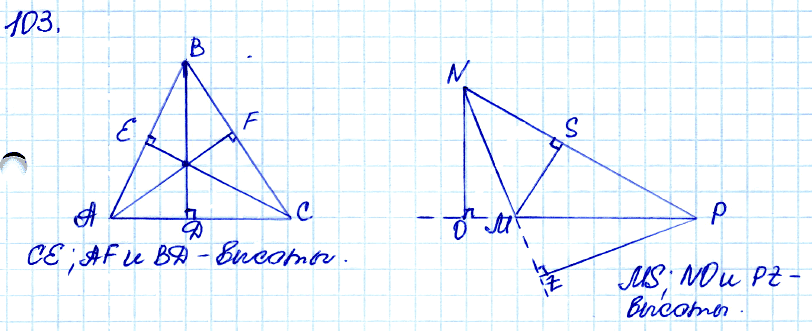
№ 103. Начертите треугольник АВС с тремя острыми углами и треугольник MNP, у которого угол М тупой. С помощью чертёжного угольника проведите высоты каждого треугольника.
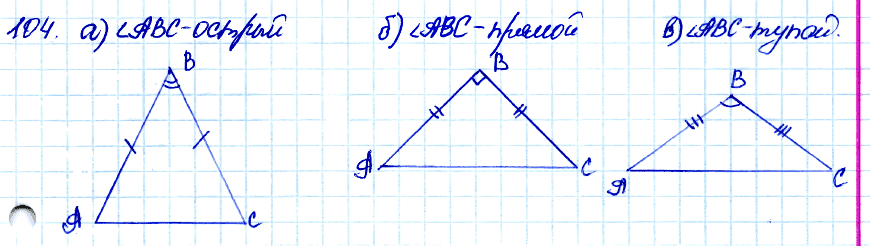
№ 104. Начертите три равнобедренных треугольника так, чтобы угол, лежащий против основания, был: а) острым; б) прямым; в) тупым.
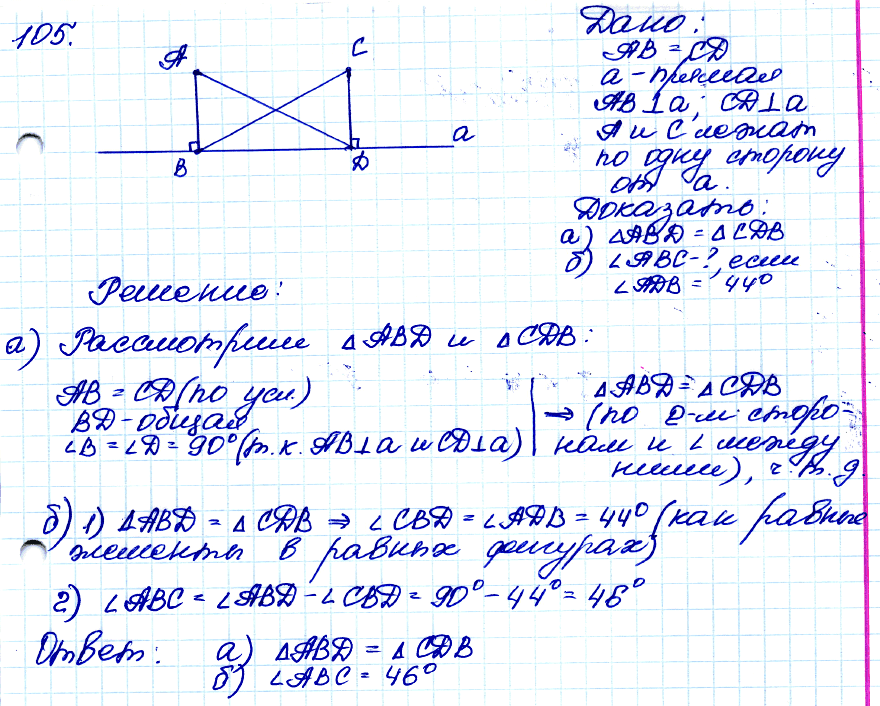
№ 105. □ Точки А и С лежат по одну сторону от прямой а. Перпендикуляры АВ и CD к прямой а равны.
а) Докажите, что ∠ABD = ∠CDB; б) найдите ∠ABC, если ∠ADB = 44°.
№ 106. □ Медиана AD треугольника АВС продолжена за точку D на отрезок DE, равный AD, и точка Е соединена с точкой С.
а) Докажите, что ΔABD = ΔECD; б) найдите ∠ACE, если ∠ACD = 56°, ∠ABD = 40°.
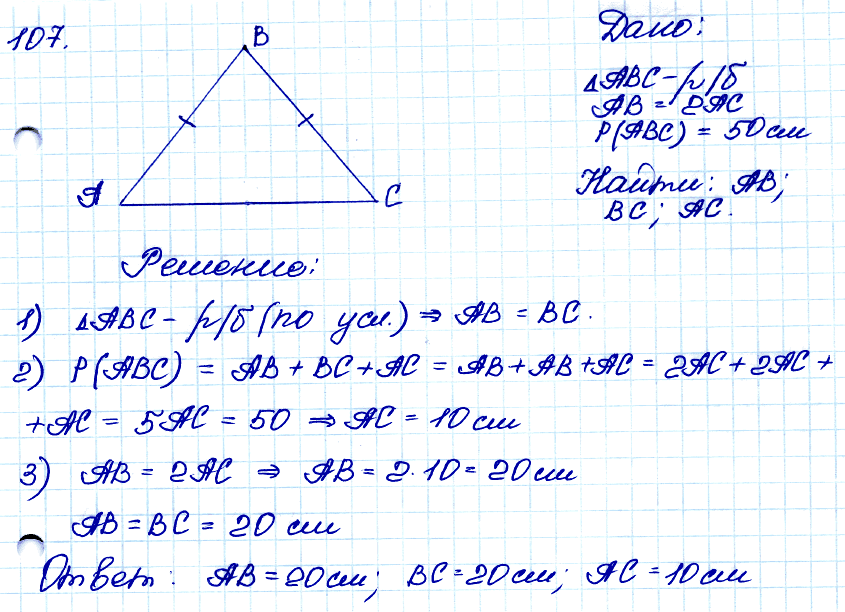
№ 107. □ В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметр равен 50 см. Найдите стороны треугольника.
№ 108. □ Периметр равнобедренного треугольника АВС с основанием ВС равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны АВ и ВС.
№ 109. □ В равнобедренном треугольнике АВС с основанием ВС проведена медиана AM. Найдите медиану AM, если периметр треугольника АВС равен 32 см, а периметр треугольника АВМ равен 24 см.
№ 110. □ Докажите, что если медиана треугольника является его высотой, то треугольник равнобедренный.
№ 111. □ На рисунке 65 CD = BD, ∠1 =∠2. Докажите, что треугольник АВС равнобедренный.
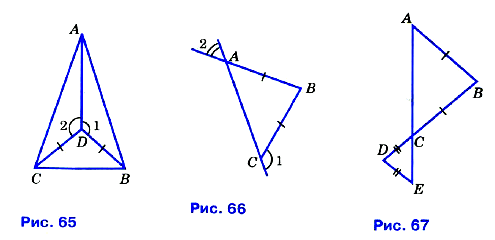
№ 112. □ На рисунке 66 АВ = ВС, ∠1 = 130°. Найдите ∠2.
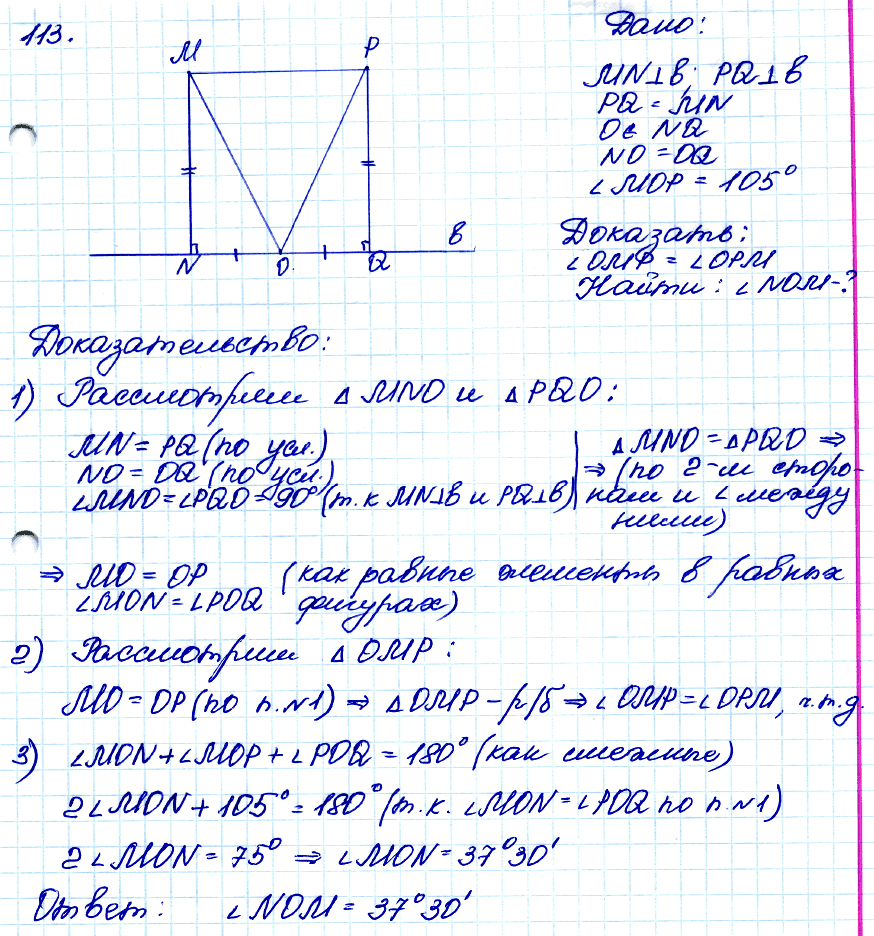
№ 113. Точки М и Р лежат по одну сторону от прямой b. Перпендикуляры MN и PQ, проведённые к прямой b, равны. Точка О — середина отрезка NQ.
а) Докажите, что ∠OMP = ∠OPM; б) найдите ∠NOM, если ∠MOP= 105°.
№ 114. □ Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны.
№ 115. Медиана AM треугольника АВС равна отрезку ВМ. Докажите, что один из углов треугольника АВС равен сумме двух других углов.
№ 116. □ Докажите, что в равностороннем треугольнике все углы равны.
№ 117. □ На рисунке 67 АВ = ВС, CD = DE. Докажите, что ∠BAC = ∠CED.
№ 118. На основании ВС равнобедренного треугольника АВС отмечены точки М и N так, что ВМ = CN. Докажите, что: а) ΔВАМ = ΔСAN; б) треугольник AMN равнобедренный.
№ 119. □ В равнобедренном треугольнике DEK с основанием DK = 16 см отрезок EF — биссектриса, ∠DEF = 43°. Найдите KF, ∠DEK, ∠EFD.
№ 120. □ В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. На сторонах АВ и СВ отмечены соответственно точки Е и F так, что AE = CF. Докажите, что: a) ΔBDE = ΔBDF; б) ΔADE = ΔCDF.
Вы смотрели: Практические задания и задачи №№ 100-120 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 2. Медианы, биссектрисы и высоты треугольника. (16. Перпендикуляр к прямой. 17. Медианы, биссектрисы и высоты треугольника. 18. Свойства равнобедренного треугольника). Геометрия Атанасян Задачи 100-120 + Ответы.


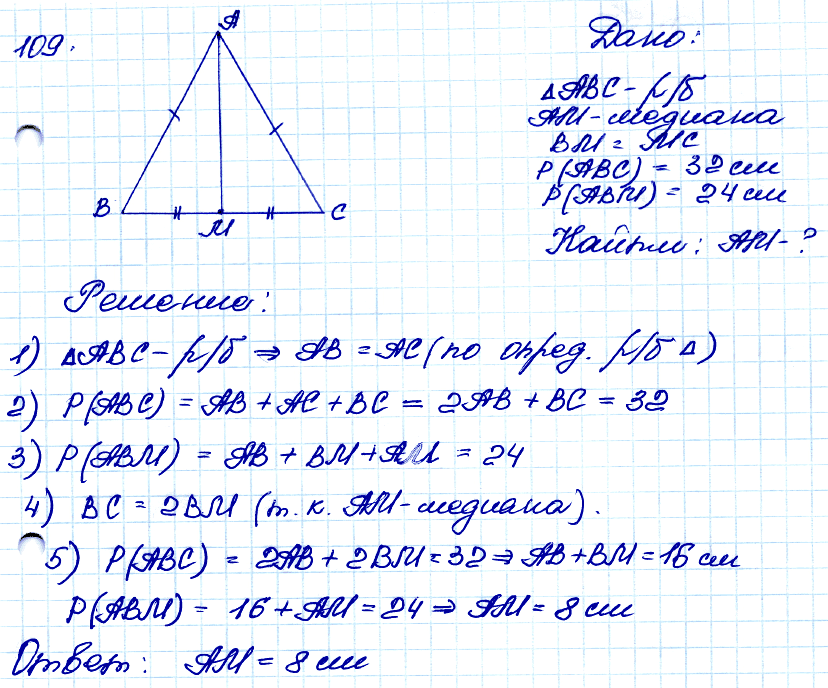










Грамотное, чёткое, аккуратное оформления решения задач- это очень важно для детей.
Есть образец решения и ребенку все понятно.
Большое спасибо.