Практические задания и задачи №№ 121-142 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 3. Второй и третий признаки равенства треугольников (19. Второй признак равенства треугольников. 20. Третий признак равенства треугольников). Геометрия Атанасян Задачи 121-142 + Ответы.
◄ Задачи 100-120 ОГЛАВЛЕНИЕ учебника Задачи 143-155 ►
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Геометрия 7 класс (УМК Атанасян)
Практические задания
и задачи №№ 121-142
№ 121. □ Отрезки АВ и CD пересекаются в середине О отрезка АВ, ∠OAD = ∠OBC.
а) Докажите, что ΔСВО = ΔDAO; б) найдите ВС и СО, если CD = 26 см, AD = 15 см.
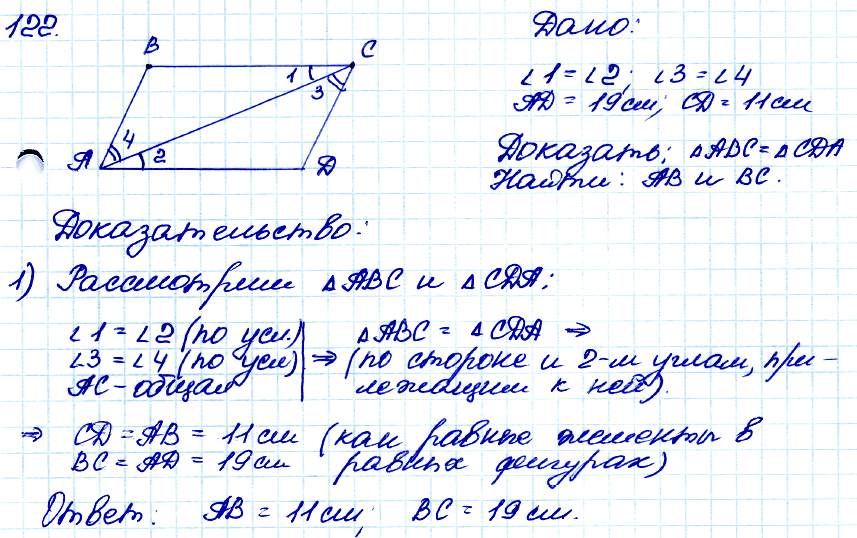
№ 122. □ На рисунке 53 ∠1 = ∠2, ∠3 = ∠4.
а) Докажите, что ΔАВС = ΔCDA; б) найдите АВ и ВС, если АО =19 см, CD = 11 см.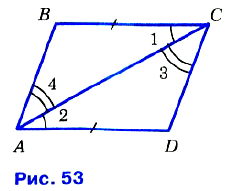
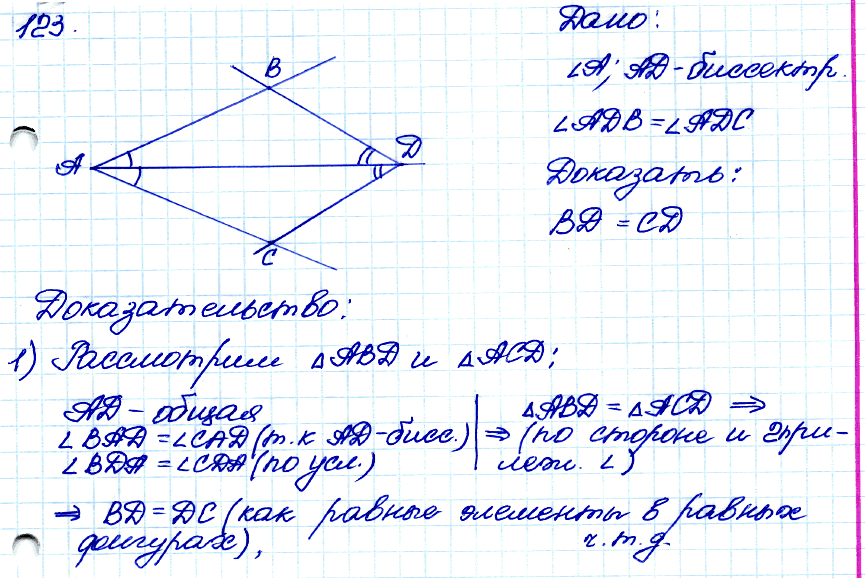
№ 123. □ На биссектрисе угла А взята точка D, а на сторонах этого угла — точки В и С такие, что ∠ADB = ∠ADC. Докажите, что BD = CD.
№ 124. □ По данным рисунка 73 докажите, что ОР = ОТ, ∠P = ∠T.
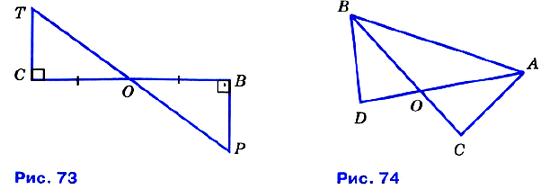
№ 125. □ На рисунке 74 ∠DAC = ∠DBC, АО = ВО. Докажите, что ∠C = ∠D и AC = BD.
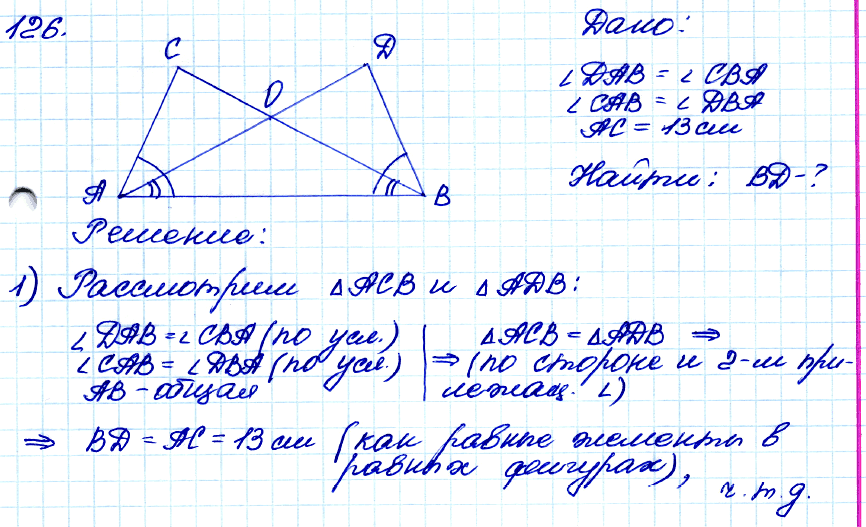
№ 126. □ На рисунке 74 ∠DAB = ∠CBA, ∠CAB = ∠DBA, АС =13 см. Найдите BD.
№ 127. В треугольниках АВС и А1В1С1, АВ = А1В1, ВС = В1С1, ∠B = ∠B1. На сторонах АВ и A1B1, отмечены точки D и D1 так, что ∠ACD = ∠A1C1D1. Докажите, что ΔBCD = ΔB1C1D1.
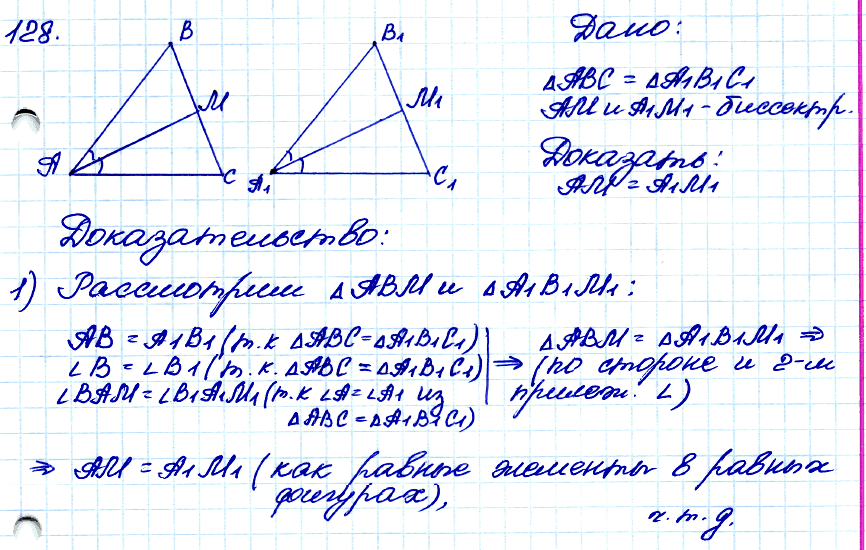
№ 128. Докажите, что в равных треугольниках биссектрисы, проведённые к соответственно равным сторонам, равны.
№ 129. Отрезки АС и BD пересекаются в середине О отрезка АС, ∠BCO = ∠DAO. Докажите, что ΔВОА = ΔDOC.
№ 130. В треугольниках АВС и А1В1С1, отрезки СО и С1О1 — медианы, BC = B1C1, ∠B = ∠B1 и ∠C = ∠C1. Докажите, что: а) ΔАСО = ΔА1С1О1; б) ΔВСO = ΔВ1С1O1.
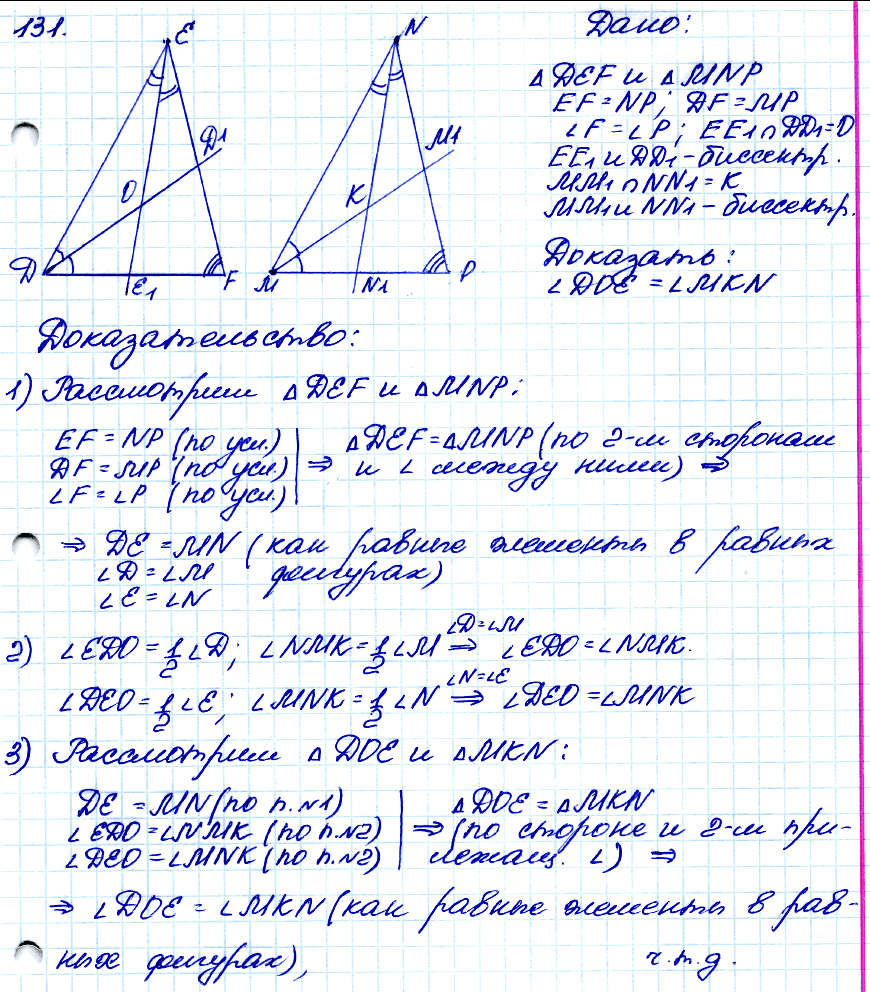
№ 131. В треугольниках DEF и MNP EF = NP, DF = MP и ∠F = ∠P. Биссектрисы углов Е и D пересекаются в точке О, а биссектрисы углов М и N — в точке К. Докажите, что ∠DOE = ∠MKN.
№ 132. Прямая, перпендикулярная к биссектрисе угла А, пересекает стороны угла в точках М и N. Докажите, что треугольник AMN — равнобедренный.
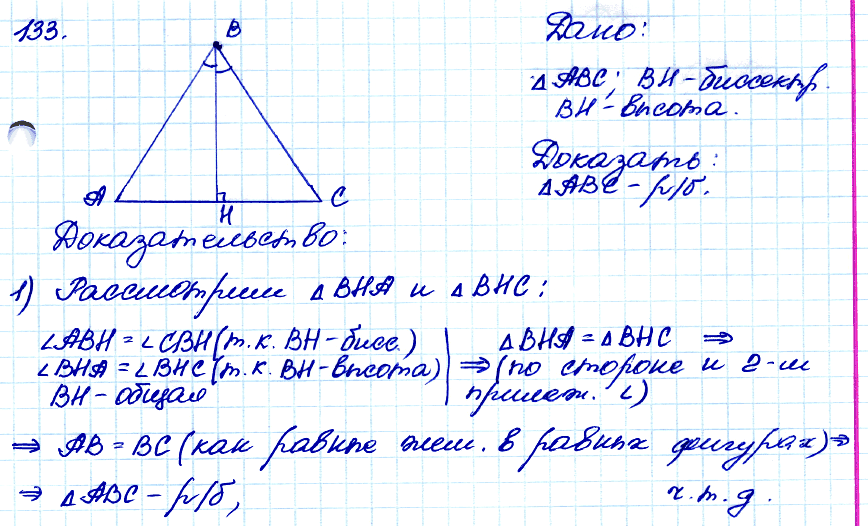
№ 133. Докажите, что если биссектриса треугольника является его высотой, то треугольник — равнобедренный.
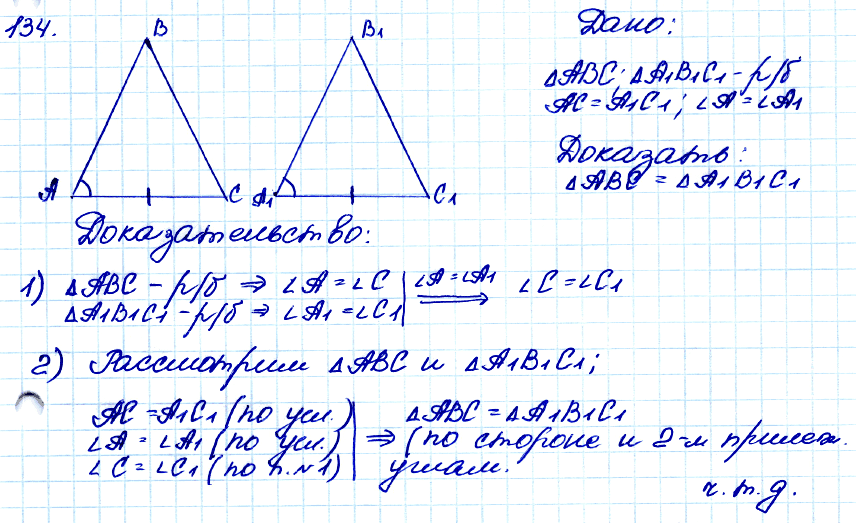
№ 134. Докажите, что равнобедренные треугольники равны, если основание и прилежащий к нему угол одного треугольника соответственно равны основанию и прилежащему к нему углу другого треугольника.
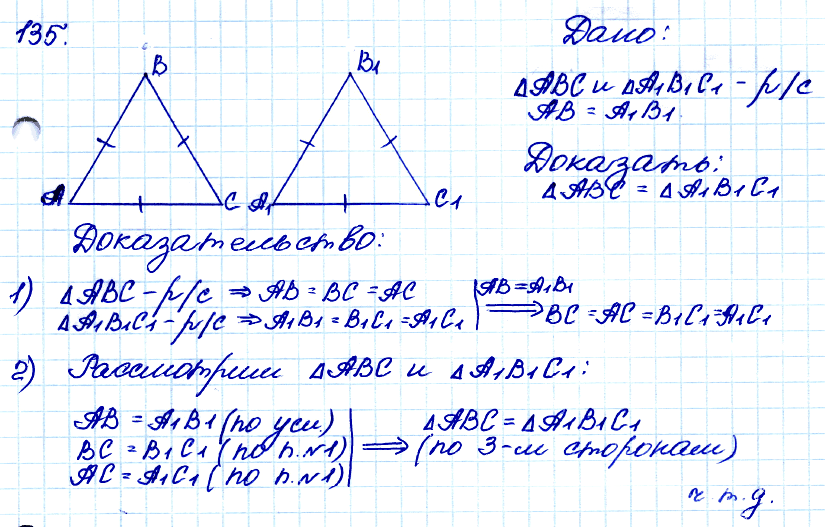
№ 135. Докажите, что если сторона одного равностороннего треугольника равна стороне другого равностороннего треугольника, то треугольники равны.
№ 136. □ На рисунке 52 АВ = АС, BD = DC и ∠BAC = 50°. Найдите ∠CAD.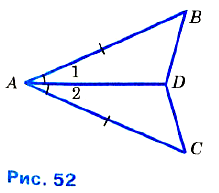
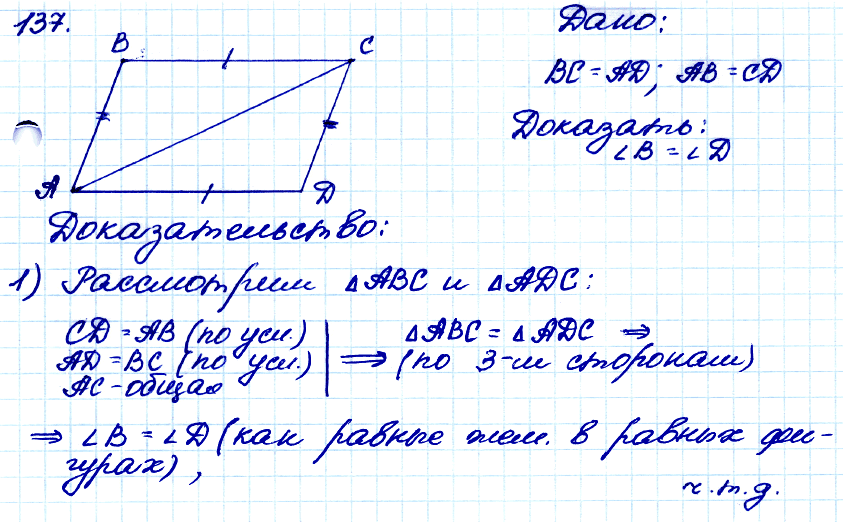
№ 137. На рисунке 53 BC = AD, AB = CD. Докажите, что ∠B = ∠D.
№ 138. На рисунке 75 AB = CD и BD = АС. Докажите, что: a) ∠CAD = ∠ADB; б) ∠BAC = ∠CDB.
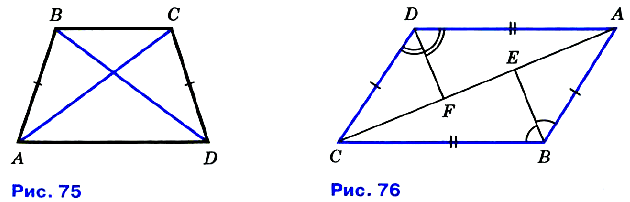
№ 139. На рисунке 76 АВ = CD, AD = BC, BE — биссектриса угла ABC, a DF — биссектриса угла ADC. Докажите, что: а) ∠ABE = ∠ADF; б) ΔАВЕ = ΔCDF.
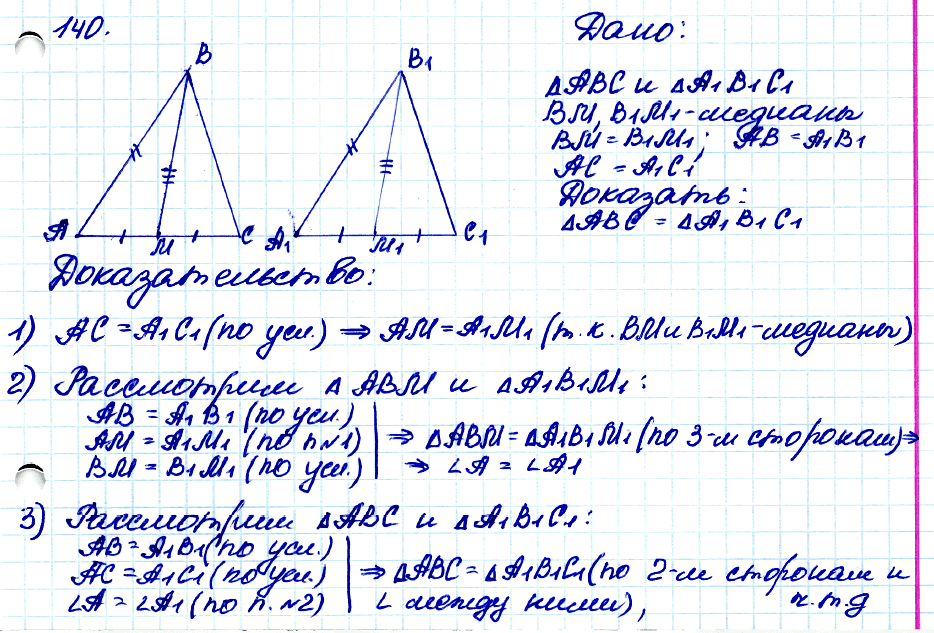
№ 140. В треугольниках АВС и А1В1С1 медианы ВМ и В1М1 равны, АВ = А1В1 и АС = А1С1. Докажите, что ΔАВС = ΔА1В1С1.
№ 141. В треугольниках АВС и А1В1С1 отрезки AD и A1D1 — биссектрисы, АВ = А1В1, BD = B1D1 и AD = A1D1. Докажите, что ΔАВС = ΔА1В1С1.
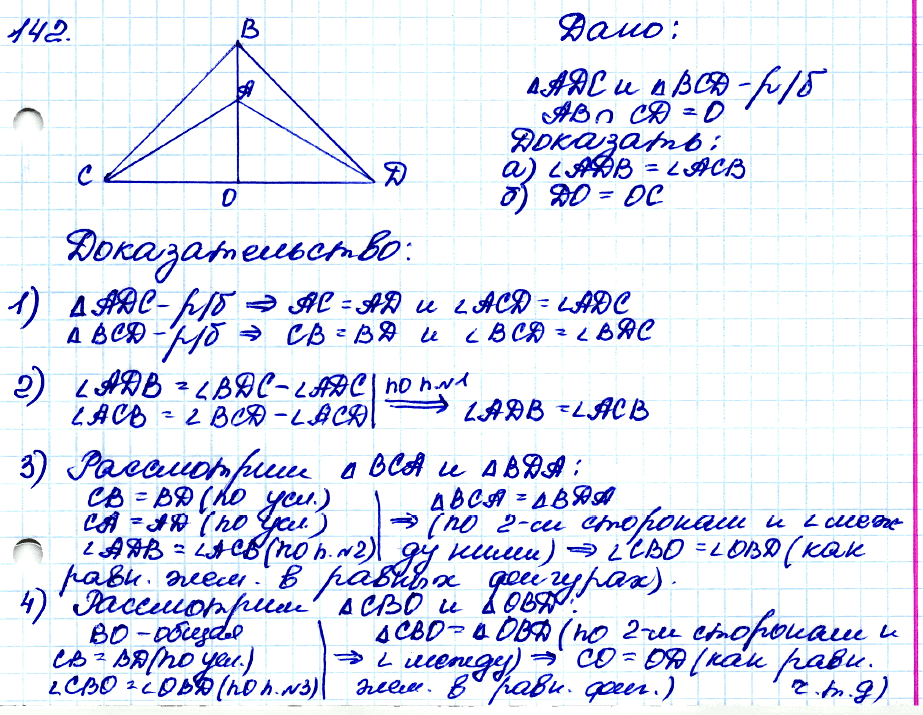
№ 142. Равнобедренные треугольники ADC и BCD имеют общее основание DC. Прямая АВ пересекает отрезок CD в точке О. Докажите, что: a) ∠ADB = ∠ACB; б) DO = OC.
Вы смотрели: Практические задания и задачи №№ 121-142 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 3. Второй и третий признаки равенства треугольников (19. Второй признак равенства треугольников. 20. Третий признак равенства треугольников). Геометрия Атанасян Задачи 121-142 + Ответы.