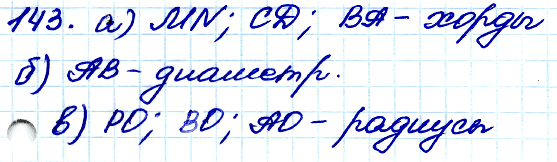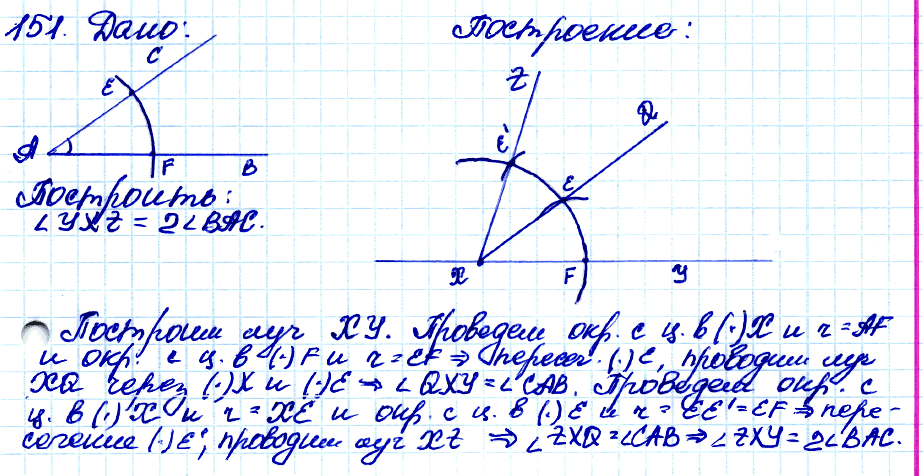Практические задания и задачи №№ 143-155 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 4. Задачи на построение. (21. Окружность. 22. Построения циркулем и линейкой. 23. Примеры задач на построение). Геометрия Атанасян Задачи 143-155 + Ответы.
◄ Задачи 121-142 ОГЛАВЛЕНИЕ учебника Задачи 156-185 ►
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Геометрия 7 класс (УМК Атанасян)
Практические задания
и задачи №№ 143-155
№ 143. □ Какие из отрезков, изображённых на рисунке 90, являются: а) хордами окружности; б) диаметрами окружности; в) радиусами окружности?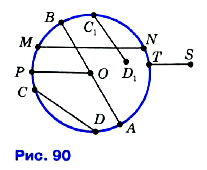
№ 144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВС равны; в) ∠BAD = ∠BCD.
№ 145. □ Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружности. Найдите ∠POM.
№ 146. □ Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, если известно, что СВ = 13 см, АВ = 16 см.
№ 147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВС — диаметр окружности. Докажите, что хорды АВ и АС равны.
№ 148. □ На прямой даны две точки А и В. На продолжении луча ВА отложите отрезок ВС так, чтобы ВС = 2АВ.
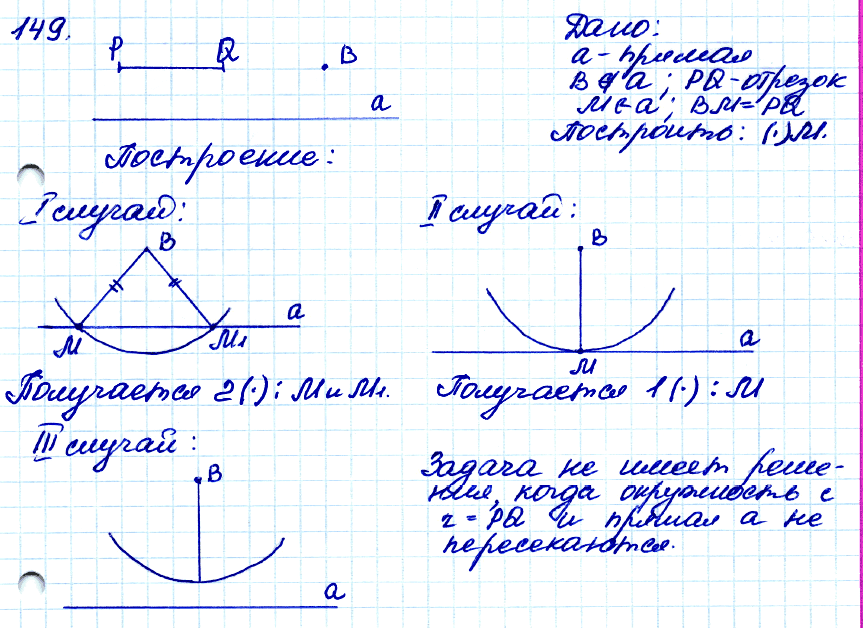
№ 149. □ Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой а так, чтобы BM = PQ. Всегда ли задача имеет решение?
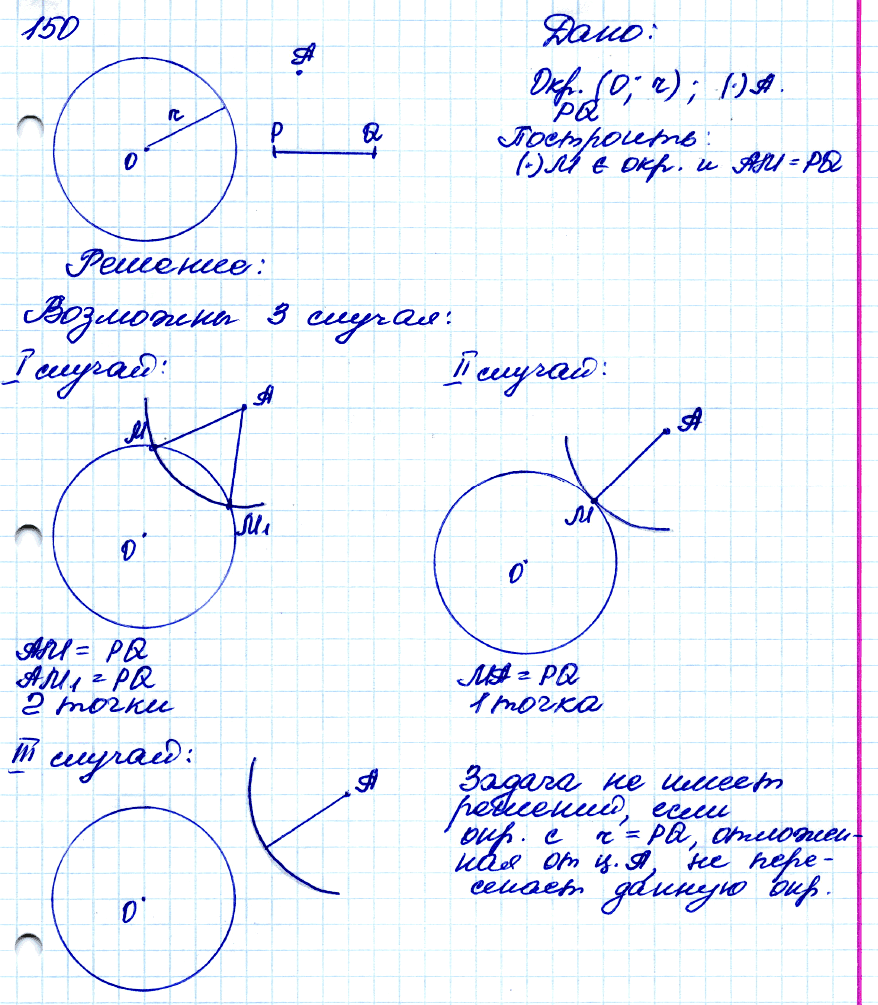
№ 150. □ Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окружности так, чтобы AM = PQ. Всегда ли задача имеет решение?
№ 151. □ Даны острый угол ВАС и луч XY. Постройте угол YXZ так, чтобы ∠YXZ = 2∠BAC.
№ 152. Дан тупой угол АОВ. Постройте луч ОХ так, чтобы углы ХОА и ХОВ были равными тупыми углами.
№ 153. □ Даны прямая а и точка М, не лежащая на ней. Постройте прямую, проходящую через точку М и перпендикулярную к прямой а.
Указание к решению. Построим окружность с центром в данной точке М, пересекающую данную прямую а в двух точках, которые обозначим буквами А и В (рис. 91). Затем построим две окружности с центрами А и В, проходящие через точку М. Эти окружности пересекаются в точке М и ещё в одной точке, которую обозначим буквой N. Проведём прямую MN и докажем, что эта прямая — искомая, т. е. она перпендикулярна к прямой а. В самом деле, треугольники AMN и BMN равны по трём сторонам, поэтому ∠1 = ∠2. Отсюда следует, что отрезок МС (С — точка пересечения прямых а и MN) является биссектрисой равнобедренного треугольника АМВ, а значит, и высотой. Таким образом, MN ⊥ АВ, т. е. MN ⊥ а.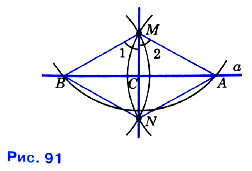
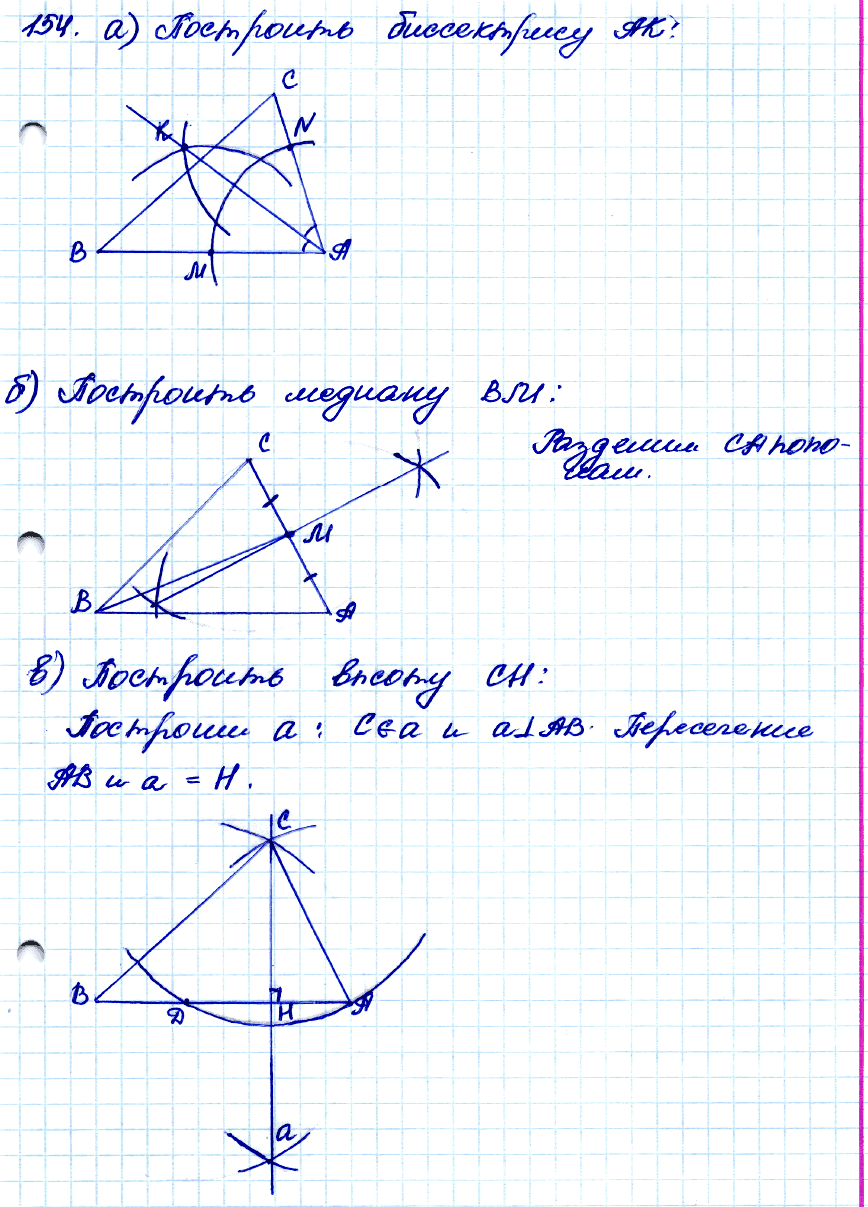
№ 154. □ Дан треугольник АВС. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.
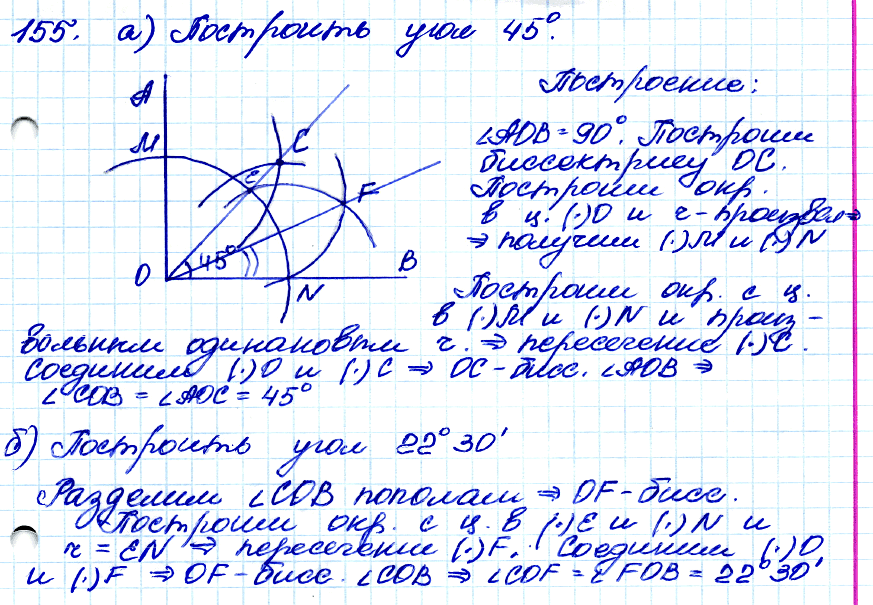
№ 155. □ С помощью циркуля и линейки постройте угол, равный: а) 45°; б) 22°30′.
Вы смотрели: Практические задания и задачи №№ 143-155 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе II «ТРЕУГОЛЬНИКИ»: § 4. Задачи на построение. (21. Окружность. 22. Построения циркулем и линейкой. 23. Примеры задач на построение). Геометрия Атанасян Задачи 143-155 + Ответы.