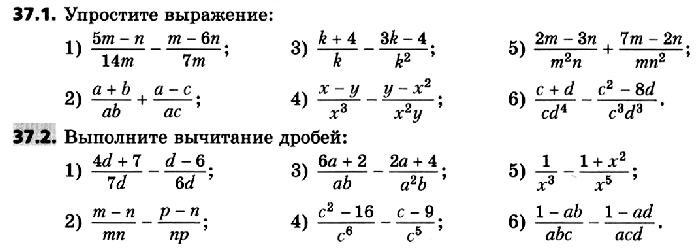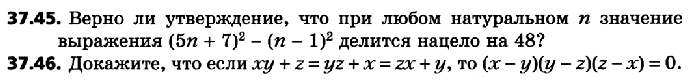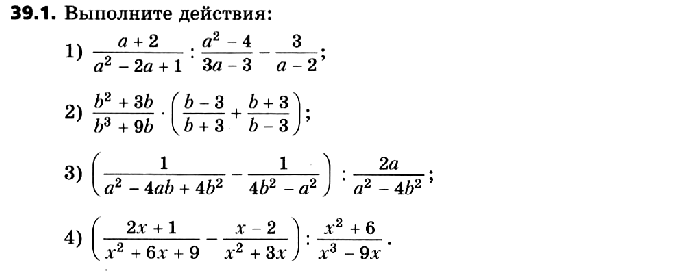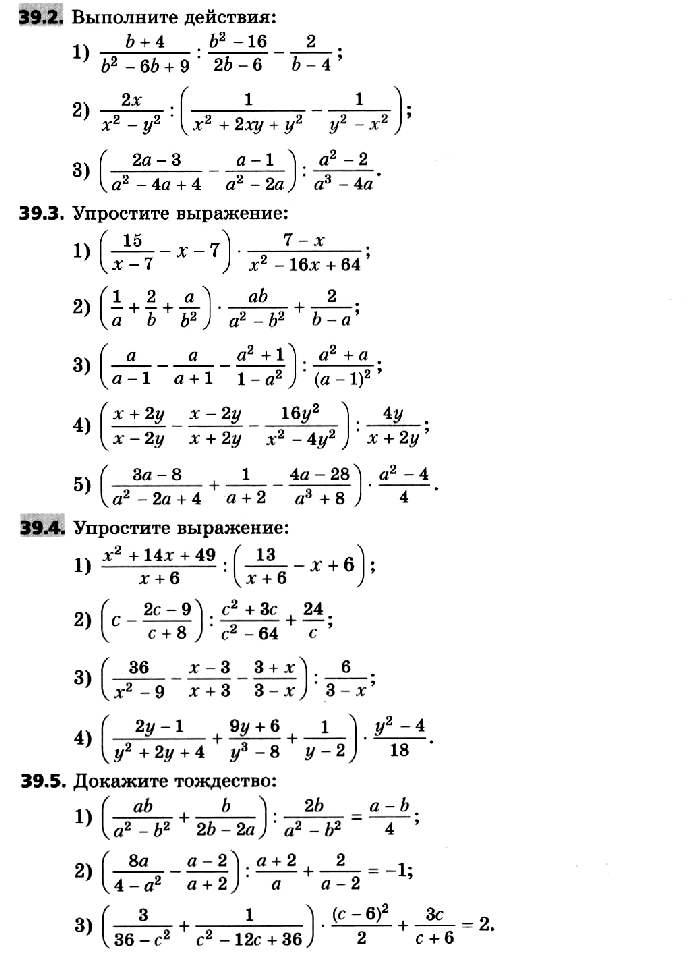Алгебра 7 класс УМК Мерзляк, Поляков (угл.) онлайн. В учебных целях использованы цитаты из пособия «Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник)». Ознакомительный фрагмент для покупки пособия. Глава 5. Рациональные выражения (§37 — §39). Алгебра 7 Мерзляк (угл.) Глава 5 §§37-39.
Глава 5. Рациональные выражения (§37-§39)
§ 37. Сложение и вычитание рациональных
дробей с разными знаменателями
Так же как и в случае с обыкновенными дробями, применяя основное свойство рациональной дроби, сложение и вычитание дробей с разными знаменателями можно свести к сложению и вычитанию дробей с одинаковыми знаменателями.
Пусть надо сложить две рациональные дроби А/В и C/D.
Можно записать: A/B = (A • D) / (B • D); C/D = (C • B) / (D • B).
Тогда A/B + C/D = (A • D) / (B • D) + (C • B) / (D • B) = (A • D + C • B) / (B • D).
Здесь в качестве общего знаменателя выбрано выражение, равное произведению знаменателей данных дробей. Заметим, что произведение знаменателей данных дробей не всегда является наиболее удобным общим знаменателем.
Напомним, что при нахождении общего знаменателя обыкновенных дробей мы находили наименьшее общее кратное знаменателей, раскладывая их на простые множители. Аналогично для нахождения общего знаменателя рациональных дробей может оказаться удобным предварительно разложить знаменатели на множители.


Заметим, что сумма и разность двух рациональных дробей являются рациональными дробями.
- Как выполнить сложение и вычитание рациональных дробей с разными знаменателями?
- Что является суммой и разностью двух рациональных дробей?
Упражнения 37.1 — 37.46
§ 38. Умножение и деление рациональных дробей.
Возведение рациональной дроби в степень
Вы знаете правила умножения и деления обыкновенных дробей. Их можно выразить следующими равенствами:
а/b • с/d = ас/bd; а/b : с/d = ad/bc. Аналогично выполняют умножение и деление рациональных дробей.
■ Произведением двух рациональных дробей является рациональная дробь, числитель которой равен произведению числителей данных дробей, а знаменатель — произведению их знаменателей.
■ Частным двух рациональных дробей является рациональная дробь, числитель которой равен произведению числителя делимого и знаменателя делителя, а знаменатель — произведению знаменателя делимого и числителя делителя.


■ Чтобы возвести рациональную дробь в степень, надо возвести в эту степень числитель и знаменатель. Первый результат записать как числитель, а второй — как знаменатель дроби.
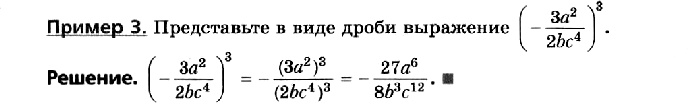
- Какая дробь является произведением двух рациональных дробей?
- Какая дробь является частным двух рациональных дробей?
- Как возвести рациональную дробь в степень?
Упражнения 38.1–38.35
§ 39. Тождественные преобразования
рациональных выражений
Правила действий над рациональными дробями позволяют любое рациональное выражение преобразовать в рациональную дробь. Рассмотрим примеры.
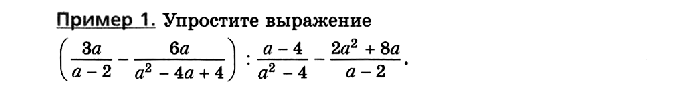


Упражнения 39.1–39.30
39.27. На первом складе было картофеля в 3 раза больше, чем на втором. Когда с первого склада вывезли 400 кг картофеля, то на нём осталось картофеля в 2 раза меньше, чем было на втором. Сколько килограммов картофеля было на первом складе сначала?
39.28. Куртка стоила на 1500 р. меньше, чем костюм. Во время сезонной распродажи куртка подешевела на 10 %, а костюм — на 20 %, после чего куртку и костюм можно было приобрести за 8000 р. Какова первоначальная цена куртки и какова — костюма?
39.29. Рабочий должен был изготовлять ежедневно 10 деталей. Однако он изготовлял ежедневно 12 деталей, и уже за 2 дня до окончания срока работы ему осталось изготовить 6 деталей. Сколько деталей должен был изготовить рабочий?
39.30. (Из русского фольклора.) За 30 монет купили 30 птиц. Сколько купили птиц каждого вида, если за трёх воробьёв платили одну монету, за двух голубей — тоже одну монету, а за одну горлицу — две монеты, при этом купили хотя бы одну птичку каждого вида?
Вы смотрели: Алгебра 7 Мерзляк (угл.) Глава 5 §§37-39. В учебных целях использованы цитаты из пособия «Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник)». Ознакомительный фрагмент для покупки пособия. Глава 5. Рациональные выражения (§37 — §39).