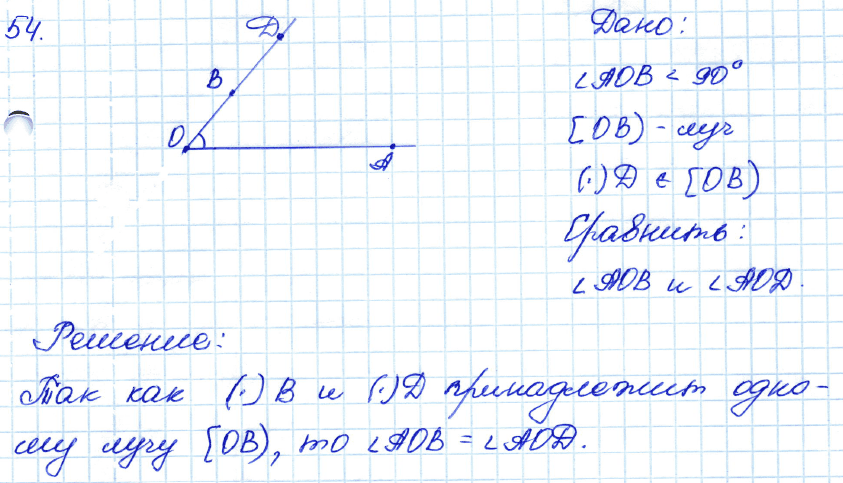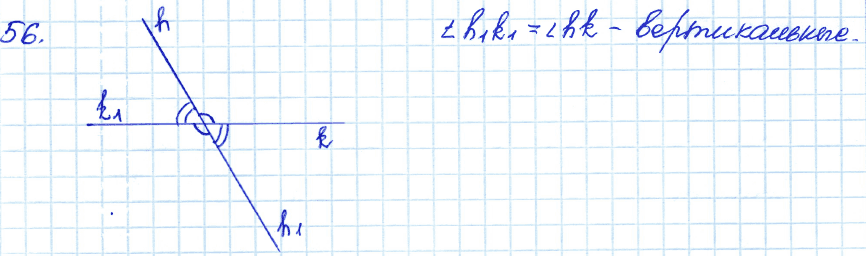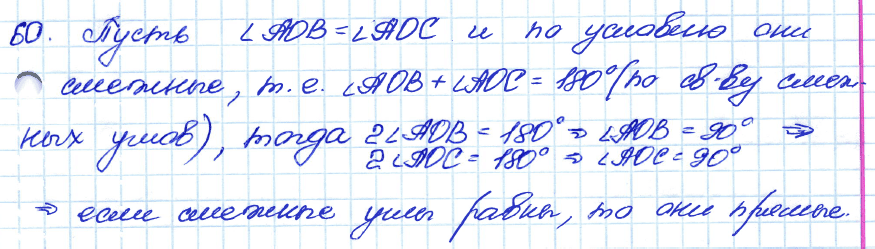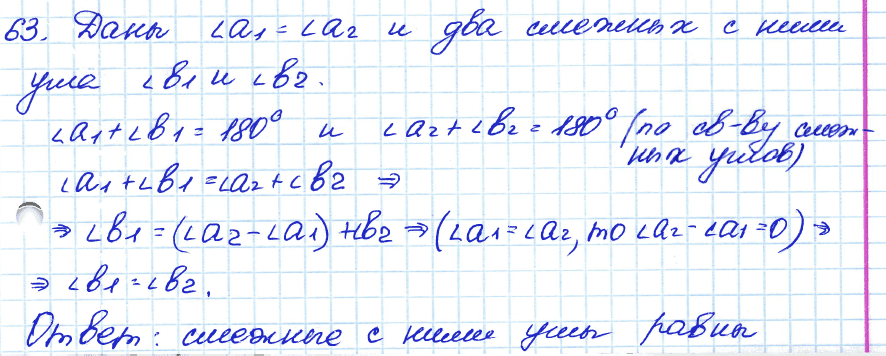Практические задания и задачи №№ 54 — 70 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения»: § 6. Перпендикулярные прямые. (11. Смежные и вертикальные углы. 12. Перпендикулярные прямые. 13. Построение прямых углов на местности). Геометрия 7 Атанасян Задачи 54-70 + Ответы.
Задачи 41-53 ОГЛАВЛЕНИЕ учебника Задачи 71-86
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Геометрия 7 класс (УМК Атанасян)
Практические задания и задачи 54-70
№ 54. Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.
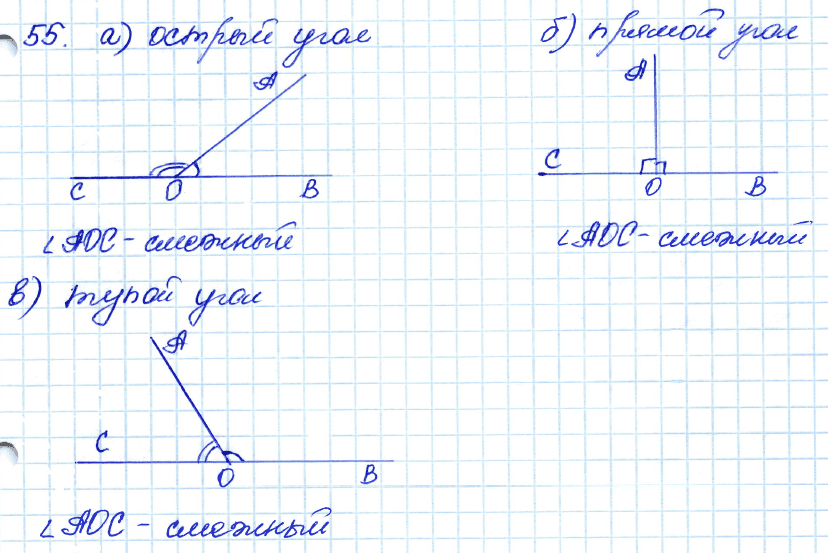
№ 55. Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.
№ 56. Начертите неразвёрнутый угол hk. Постройте угол h1k1 так, чтобы углы hk и h1k1, были вертикальными.
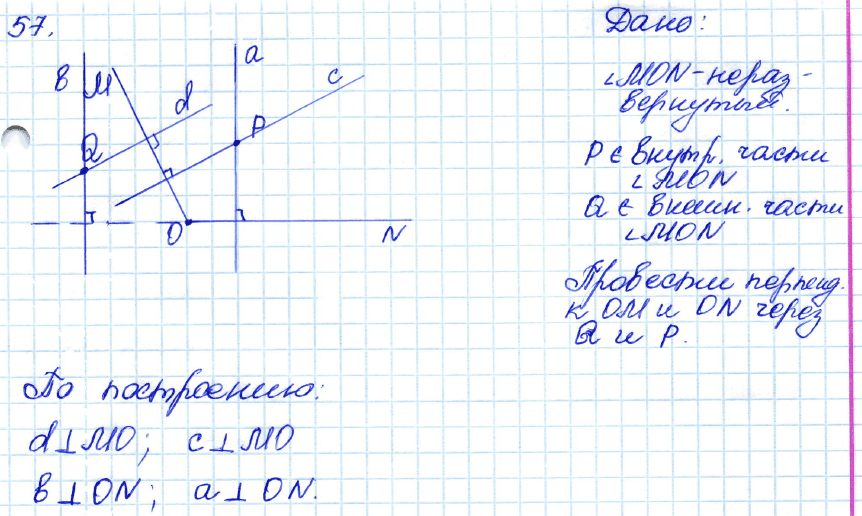
№ 57. Начертите неразвёрнутый угол MON и отметьте точку Р внутри угла и точку Q — вне его. С помощью чертёжного угольника и линейки через точки Р и Q проведите прямые, перпендикулярные к прямым ОМ и ON.
№ 58. □ Найдите угол, смежный с углом АВС, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
№ 59. □ Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
№ 60. □ Верно ли утверждение: если смежные углы равны, то они прямые?
№ 61. Найдите смежные углы hk и kl, если: а) ∠hk меньше ∠kl на 40°; б) ∠hk больше ∠kl на 120°; в) ∠hk больше ∠kl на 47°18′; г) ∠hk = 3∠kl; д) ∠hk : ∠kl = 5:4.
№ 62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
№ 63. Даны два равных угла. Равны ли смежные с ними углы?
№ 64. □ Найдите изображённые на рисунке 41 углы: а) 1, 3, 4, если ∠2 = 117°; б) 1, 2, 4, если ∠3 = 43°27′.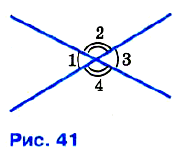
№ 65. □ Найдите неразвёрнутые углы, образованные при пересечении двух прямых, если: а) сумма двух из них равна 114°; б) сумма трёх углов равна 220°.
№ 66. □ На рисунке 41 найдите углы 1, 2, 3, 4, если: а) ∠2 + ∠4 = 220°; б) 3 (∠1 +∠3) = ∠2 + ∠4; в) ∠2 – ∠1 = 30°.
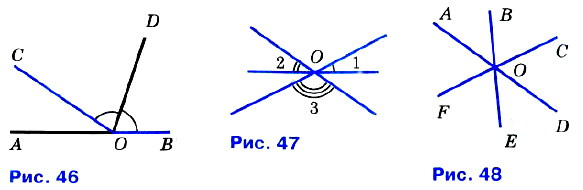
№ 67. □ На рисунке 47 изображены три прямые, пересекающиеся в точке О. Найдите сумму углов: ∠1 + ∠2 + ∠3.
№ 68. На рисунке 48 ∠AOB = 50°, ∠FOE = 70°. Найдите углы АОС, BOD, СОЕ и COD.
№ 69. □ Прямая а пересекает стороны угла А в точках Р и Q. Могут ли обе прямые АР и AQ быть перпендикулярными к прямой а?
№ 70. □ Через точку А, не лежащую на прямой а, проведены три прямые, пересекающие прямую а. Докажите, что по крайней мере две из них не перпендикулярны к прямой а.
Вы смотрели: Практические задания и задачи №№ 54 — 70 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения»: § 6. Перпендикулярные прямые. (11. Смежные и вертикальные углы. 12. Перпендикулярные прямые. 13. Построение прямых углов на местности). Геометрия 7 Атанасян Задачи 54-70.