Геометрия 7 класс для любого УМК. Диагностическая работа № 2 по геометрии за 1-е полугодие для тренировки при подготовке к контрольным и диагностическим работам.
ПРОМЕЖУТОЧНАЯ
ДИАГНОСТИЧЕСКАЯ РАБОТА № 2
В задачах 1–6 достаточно указать ответ.
№ 1. Какие утверждения верны?
A. Если две стороны одного треугольника равны двум сторонам другого треугольника и один из углов первого треугольника равен углу другого треугольника, то такие треугольники равны.
Б. Если сумма двух углов, имеющих общую вершину, равна 180°, то они являются смежными.
B. В любом равнобедренном треугольнике хотя бы две медианы равны между собой.
Г. Биссектриса любого треугольника делит его на две равные части.
Ответ: В.
№ 2. На рисунке изображён отрезок MN и отмечено несколько точек. Какие из отмеченных точек вместе с точками Ми N являются вершинами равнобедренного треугольника?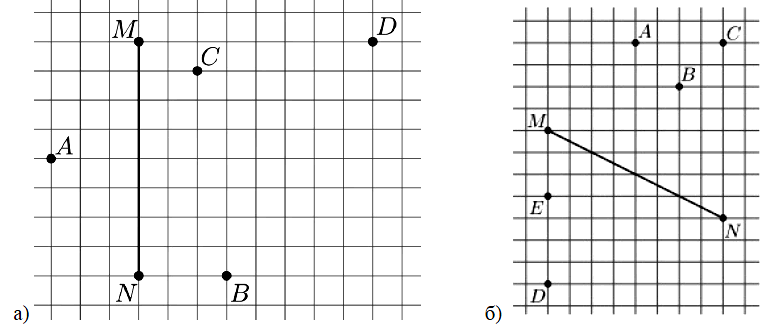
а) Ответ: A, D. б) Ответ: A, B, C.
№ 3. Лист бумаги перегнули по прямой линии и сложили так, как показано на рисунке. Один из двух отмеченных углов равен 64°. Найдите другой угол. Укажите все возможные варианты.
Ответ: 52°или 58°.
№ 4. На прямой отмечены точки A, B, C, D, E (необязательно в таком порядке) так, что расстояния между ними оказались равны: DE = 8, AE = 6, AC = 9, BC = 5, BD = 10. Изобразите, в каком порядке расположены точки, и укажите расстояния между соседними точками.
Ответ: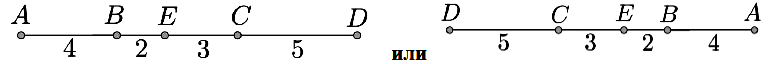 
№ 5. В некоторый момент угол между часовой и минутной стрелками часов оказался равен а. Через 5 часов он опять оказался равен а. Найдите все возможные значения а.
Ответ: 75° или 105°.
№ 6. Стороны треугольника ABC равны AB = 6, BC = 7, CA = 8. На стороне BC отмечена такая точка E, что периметр треугольника ABE на 1 больше периметра треугольника ACE. Найдите BE.
Ответ: 5.
В задачах 7–9 необходимо записать решение.
№ 7. На рисунке справа KL = LM и равны углы, отмеченные одинаково. Укажите равные треугольники. Обоснуйте их равенство.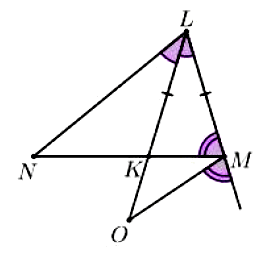
Ответ: ΔLMO = ΔLKN. Решение:
№ 8. В треугольнике ABC на стороне АС выбрана точка L и проведены высота LH треугольника ABL и биссектриса LK треугольника BLC. Оказалось, что угол KLH – прямой. Найдите AB, если AH = 6.
Ответ: 12. Решение.
1. ∠ALB + ∠CLB = 180° из свойства смежных углов,
2. ∠KLB + ∠HLB = ∠HLK = 90° (по условию),
3. LK – биссектриса угла BLC, значит, LH – биссектриса угла ALB (из пп. 1 и 2 и свойства биссектрис смежных углов)
4. В треугольнике ALB биссектриса совпала с высотой, значит, он равнобедренный.
5. В треугольнике ALB отрезок LH также является медианой, значит, AB = 2AH = 12.
№ 9. На продолжении стороны AB треугольника ABC за точку B отмечена точка K, такая что KB = AB. Продолжение медианы AM треугольника ABC за точку M пересекает отрезок CK в точке L. Оказалось, что KM = AB. Докажите, что ∠AMB = ∠KCB.
Доказательство:
Вы смотрели: Геометрия 7 класс для любого УМК. Диагностическая работа № 2 по геометрии за 1-е полугодие для тренировки при подготовке к контрольным и диагностическим работам.
(с) В учебных целях использованы цитаты из работ ГАОУ ДПО «Центр педагогического мастерства» 2021 (Математическая вертикаль).
А как у вас получилось АН=12 если по условию АН=6(в 8 задаче)????????:(
В треугольнике ALB отрезок LH также является медианой, а значит, AB = 2AH = 12 (добавлен рисунок)
Седьмом классе дети только-только начинаются изучать геометрию. Непонятно, зачем давать такие сложные задачи как 7,8,9номера?! не разумнее ли дать задачи, связанные с нахождением каких-либо элементов того же треугольника?
Эта работа среди учащихся инновационного проекта «Математическая вертикаль», поэтому задания тут посложнее, чем по УМК Атанасян.