ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019-2021). Глава 2. Линейная функция. § 9. Линейная функция и ее график. Ответы на упражнения 9.31 — 9.66.
§ 9 в учебнике ОГЛАВЛЕНИЕ § 9 в задачнике
Алгебра 7 Мордкович (упр. 9.31 — 9.66)
§ 9. Линейная функция и ее график
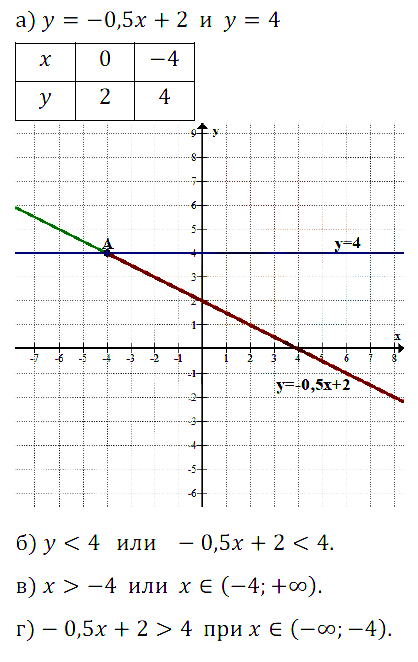
№ 9.31. Постройте график функции у = –0,5х + 2 и прямую у = 4.
а) Найдите координаты точки пересечения прямых.
б) Выделите ту часть графика функции у = –0,5х + 2, которая расположена ниже прямой у = 4. Какие значения у соответствуют выделенной части графика? Какие значения при этом принимает выражение –0,5х + 2?
в) Определите, какие значения х соответствуют выделенной части графика линейной функции.
г) Найдите, при каких значениях х выполняется неравенство –0,5х + 2 > 4.
Смотреть ответы на № 9.31
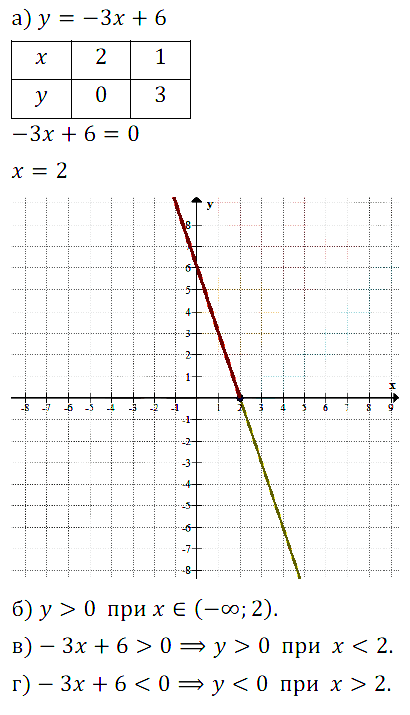
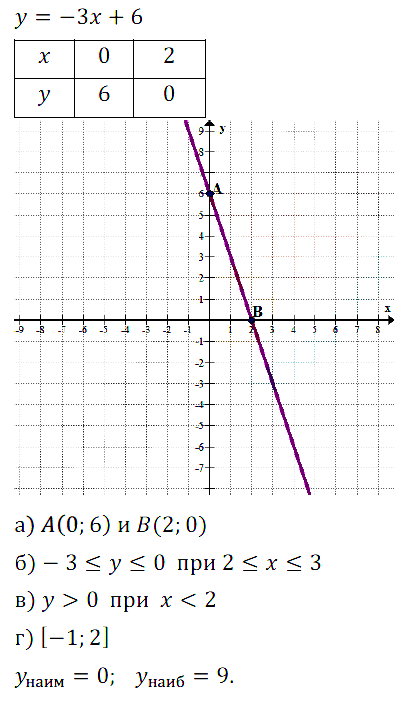
№ 9.32. Постройте график функции у = –3х + 6.
а) С помощью построенного графика решите уравнение –3х + 6 = 0.
б) Выделите ту часть графика, которая соответствует условию у > 0. Какие значения аргумента соответствуют выделенной части графика?
в) С помощью графика решите неравенство –3х + 6 > 0.
г) Решите неравенство –3х + 6 < 0.
Смотреть ответы на № 9.32
№ 9.33. Постройте график функции у = 2х – 6.
а) С помощью построенного графика решите уравнение 2х – 6 = 0.
б) Выделите ту часть графика, которая соответствует условию у < 0. При каких значениях аргумента функция принимает отрицательные значения?
в) С помощью графика решите неравенство 2х – 6 ≤ 0.
г) Решите неравенство 2х – 6 ≥ 0.
Смотреть ответы на № 9.33
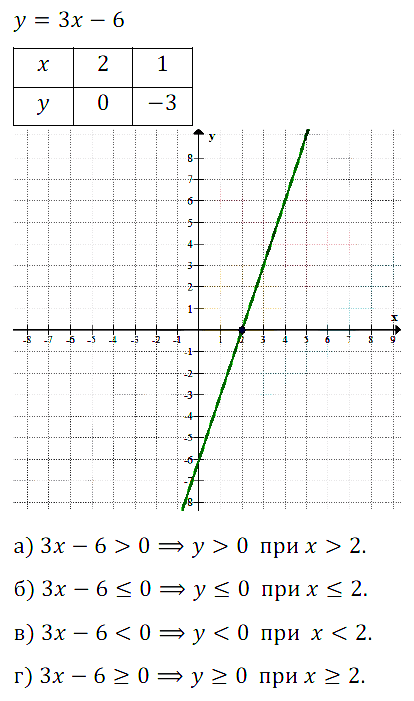
№ 9.34. Постройте график линейной функции у = 3х – 6 и с его помощью решите неравенство:
а) 3х – 6 > 0; б) 3х – 6 ≤ 0; в) 3х – 6 < 0; г) 3х – 6 ≥ 0.
Смотреть ответы на № 9.34
№ 9.35. Постройте график линейной функции у = 4х + 4 и с его помощью решите неравенство:
а) 4х + 4 > 0; б) 4х + 4 < 0; в) 4х + 4 ≤ 0; г) 4х + 4 ≥ 0.
Смотреть ответы на № 9.35
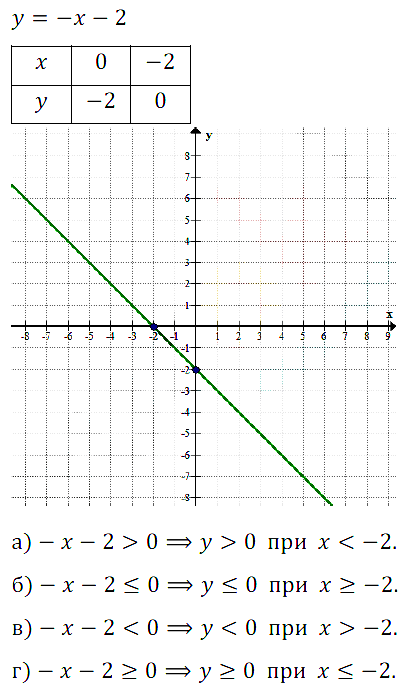
№ 9.36. Постройте график линейной функции у = –х – 2 и с его помощью решите неравенство:
а) –х – 2 > 0; б) –х – 2 < 0; в) –х – 2 < 0; г) –х – 2 > 0.
Смотреть ответы на № 9.36
№ 9.37. Постройте график линейной функции у = –2х + 4 и с его помощью решите неравенство:
а) –2х + 4 > 0; б) –2х + 4 < 0; в) –2х + 4 < 0; г) –2х + 4 > 0.
Смотреть ответы на № 9.37
Смотреть ответы на № 9.38
Смотреть ответы на № 9.39
Смотреть ответы на № 9.40
Смотреть ответы на № 9.41
Смотреть ответы на № 9.42
Смотреть ответы на № 9.43
Смотреть ответы на № 9.44
Смотреть ответы на № 9.45
Линейная функция монотонна, значит, для того чтобы найти наибольшее и наименьшее значения, нужно вычислить значения функции на концах отрезка.
а) –2 + 3 = 1, –1 + 3 = 2. Ответ: 1 — наименьшее; 2 — наибольшее.
б) –(–1) + 5 = б, –4 + 5 = 1. Ответ: 1 — наименьшее: 6 — наибольшее.
в) –3 + 3 = 0, –1 + 3 = 2. Ответ: 0 — наименьшее; 2 — наибольшее.
г) –2 + 5 = 3, –5 + 5 = 0. Ответ: 0 — наименьшее; 3 — наибольшее.
Смотреть ответы на № 9.46
Линейная функция монотонна, значит, для того чтобы найти наибольшее и наименьшее значения, нужно вычислить значения функции на концах отрезка.
а) 4 • (–1) –1 = –5, 4 • 2 – 1 = 7. Ответ: –5 – наименьшее; 7 – наибольшее.
б) –2 • 0 + 5 = 5, –2 • 4 + 5 = –3. Ответ: –3 – наименьшее; 5 – наибольшее.
в) 3 • (–l) –2 = –5, 3 • 1 – 2 = 1. Ответ: –5 – наименьшее; 1 – наибольшее.
г) –5 • 0 + 7 = 7, –5 • 2 + 7 – 3. Ответ: –3 – наименьшее; 7 – наибольшее.
Смотреть ответы на № 9.47
Смотреть ответы на № 9.48
Смотреть ответы на № 9.49
Смотреть ответы на № 9.50
Смотреть ответы на № 9.51
Смотреть ответы на № 9.52
Для того, чтобы выяснить проходит ли график функции через данную точку, нужно подставить значения абсциссы и ординаты точки в уравнение и посмотреть обращается ли уравнение в верное равенство. у = 3,2х – 5:
а) 3,2 • 3 – 5 = 4,6 – верно, значит, проходит;
б) 3,2 • 1,2 – 5 = 0 – неверно, значит, не проходит;
в) 3,2 • 7,5 – 5 = 4 – неверно, значит, не проходит;
г) 3,2 • 2,2 – 5= 2,04 – верно, значит, проходит.
Смотреть ответы на № 9.53
a) ymin = 4.
б) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наименьшего значения не существует. Наибольшее = –0,5 • (–2) + 1 = 2.
в) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наименьшее = 2,5 • 1 – 4 = –1,5. Наибольшее = 2,5 • 2 – 4 = 1.
г) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в начале промежутка стоит знак –∞, следовательно, наименьшего значения не существует. Наибольшее = 2,5 • 0 – 4 = – 4.
Смотреть ответы на № 9.54
а) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наименьшее =1/4 • (–4) + 2 = 1. Наибольшее = 1/4 • 4 + 2 = 3.
б) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наибольшего значения не существует. Наименьшее = 1/4 • 0 + 2 = 2.
в) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в начале промежутка стоит знак –∞, следовательно, наибольшего значения не существует. Наименьшее = –1/3 • 6 – 1 = –3.
г) Заданный промежуток является интервалом, следовательно, наибольшего и наименьшего значений не существует.
Смотреть ответы на № 9.55
а) х = 3х – 12; 2х = 12; х = 6. Ответ; (6; 6).
б) x = 5x + 4; 4х = –4; х = – 1. Ответ: (–1; –1).
Смотреть ответы на № 9.56
а) –х = 2х + 9; 3х = –9; х = –3. Ответ: (–3; 3).
б) –х = –3х + 8; 2х = 8; х = 4. Ответ: (4; –4).
Смотреть ответы на № 9.57
а) 2х = х + 15; х = 15;у = 2 • 15 = 30. Ответ: (15; 30).
б) у = 6y – 35; у = 7; х = 3 • 7 = 21. Ответ: (21; 7).
Смотреть ответы на № 9.58
у = –5x + m;
а) –5 • 1 + m = 2; m = 7;
б) –5 • 0,5 + m = 4; m = 6.5;
в) –5 • (–7) + m = 8; m = –27;
г) –5 • 1,2 + m = –3; m = 3.
Смотреть ответы на № 9.59
а) 3k + 4 = 5; k = 1/3;
б) k/2 + 4 = 1; k = –6;
в) –6k + 4 = –8; k = 2;
г) k/3 + 4 = –8. K = –36.
Смотреть ответы на № 9.60
Так как функция у = 2х – 3 возрастает, А = 2 • 2 – 3 = 1.
Так как функция у = 0,5x – 4 возрастает, В = 2 • 0,5 – 4 = –3.
Смотреть ответы на № 9.61
Из того, что функция у = х – 4 возрастает следует, что С = 0 – 4 = –4. Из того что функция у = 4 – х убывает следует, что D = 4 – 1 = 3. Следовательно, D > С.
Смотреть ответы на № 9.62
у = kx + m.
а) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т.с. k > 0. Но еще известно, что функция проходит через второй координатный угол. Откуда следует, что m > 0.
б) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т.е. k < 0. Но еще известно, что функция проходит через первый координатный угол. Откуда следует, что m > 0.
в) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т.е. k > 0. Но еще известно, что функция проходит через четвертый координатный угол. Откуда следует, что m < 0.
г) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т.е. k < 0. Но еще известно, что функция проходит через третий координатный угол. Откуда следует, что m < 0.
Смотреть ответы на № 9.63
y = kx + m.
а) Видно, что если мы подставим любое х > 0, то получим, что у > 0, следовательно, график функции проходит через первый координатный угол. Если же мы подставим любое х < 0, то получим, что у < 0, следовательно, график проходит через третий координатный угол. График не проходит через второй и четвертый координатные углы, (не учитывая точку (0; 0)) потому что m = 0. Ответ: график функции проходит через 1 и 3 координатные yглы.
б) Видно, что если мы подставим любое х > 0, то получим, что у < 0, следовательно, график функции проходит через первый координатный угол. Если же мы подставим любое х < 0, то получим, что у > 0, следовательно, график проходит через третий координатный угол. График не проходит через второй и четвертый координатные углы (не учитывая точку (0; 0)) потому, что m = 0. Ответ: график функции проходит через 2 и 4 координатные углы.
в) либо в первой и второй четверти, ибо в третьей и четвертой четверти;
г) совпадает с осью х.
Смотреть ответы на № 9.64
Смотреть ответы на № 9.65
Смотреть ответы на № 9.66
Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 2. Линейная функция. § 9. Линейная функция и ее график. Ответы на упражнения 9.31 — 9.66.
§ 9 в учебнике ОГЛАВЛЕНИЕ § 9 в задачнике
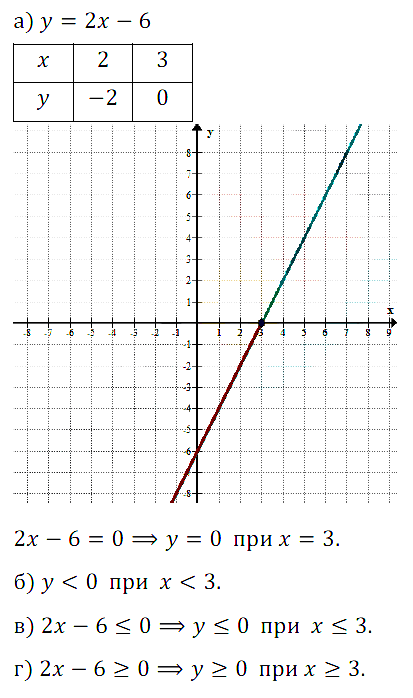
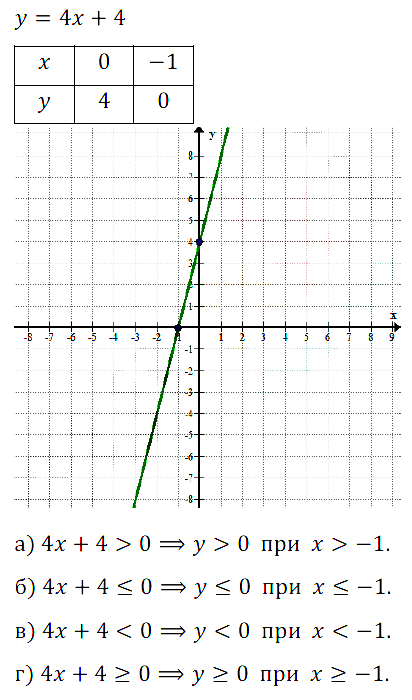
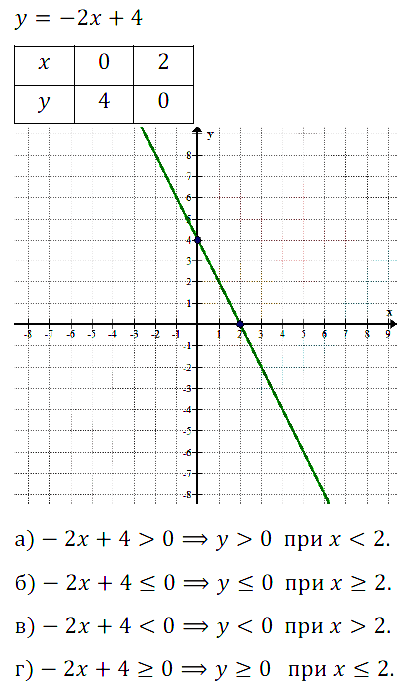
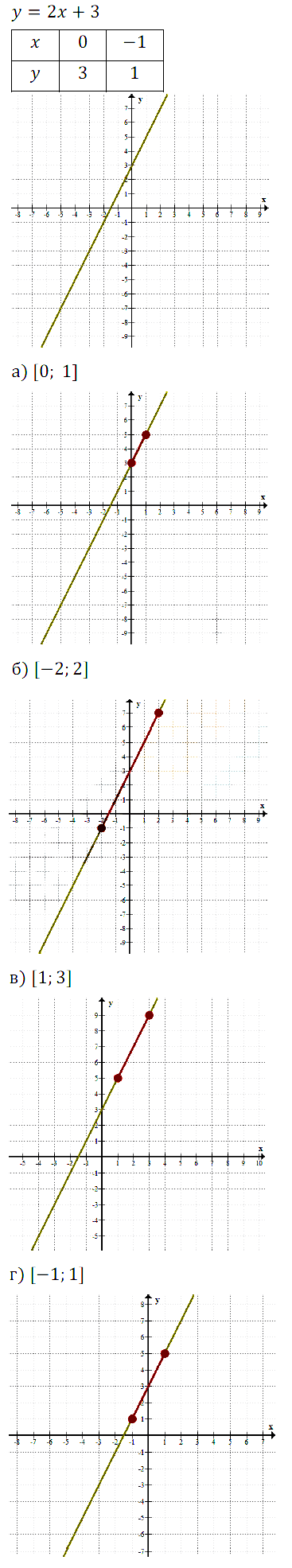
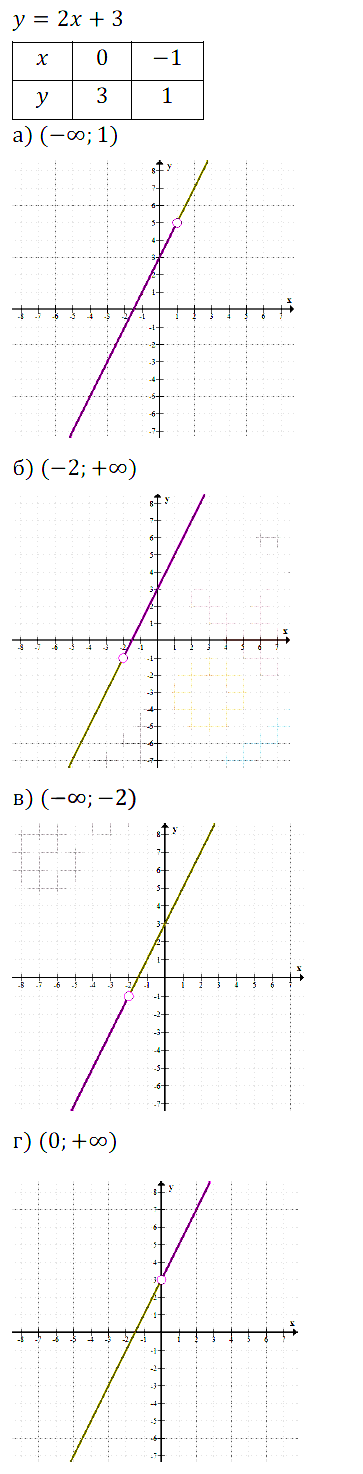
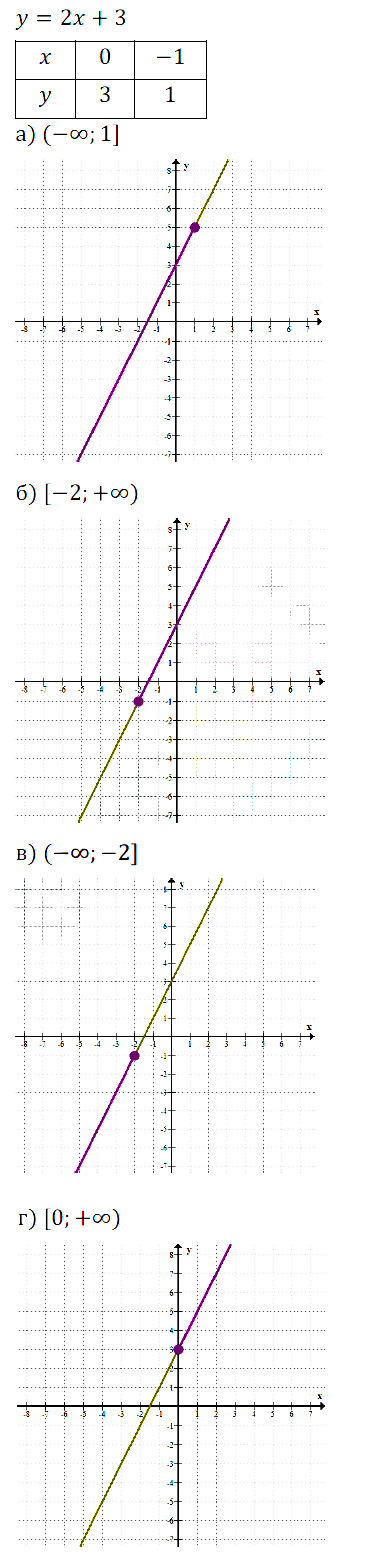
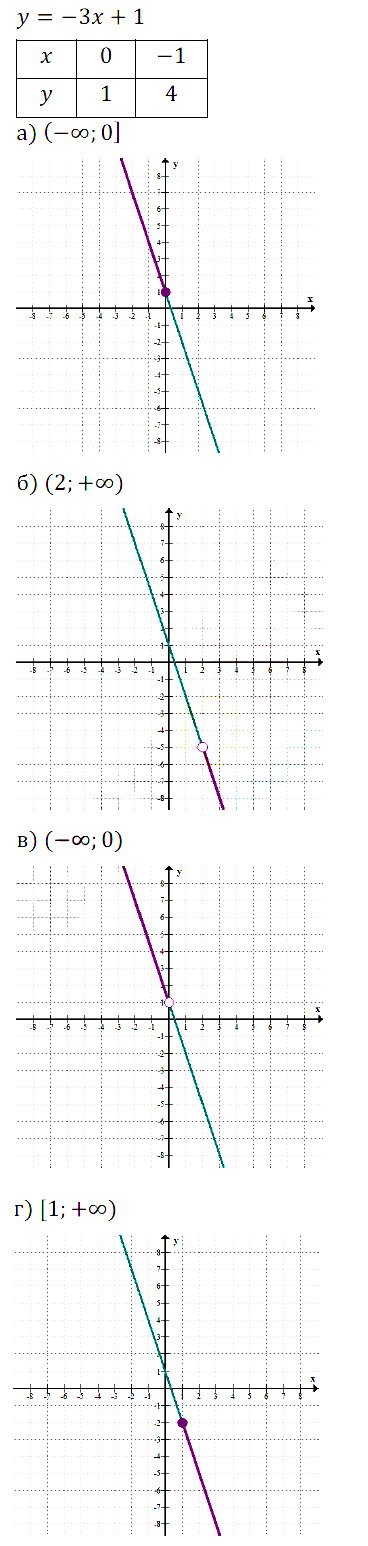
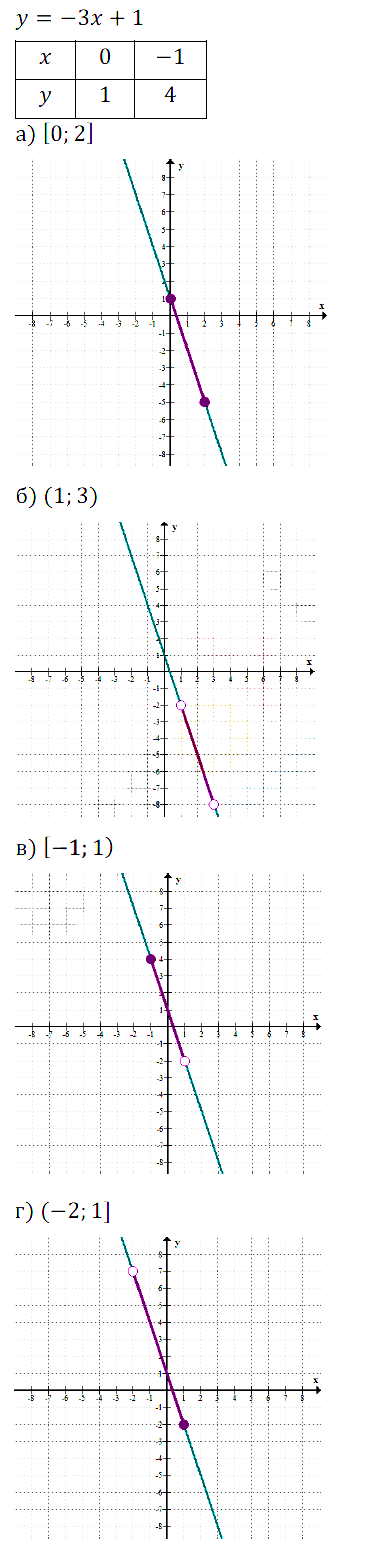
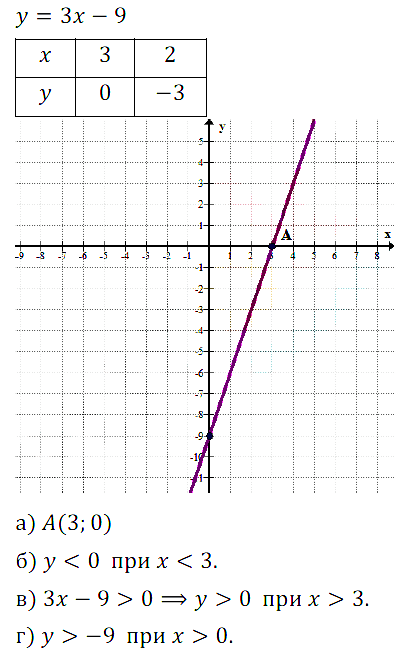
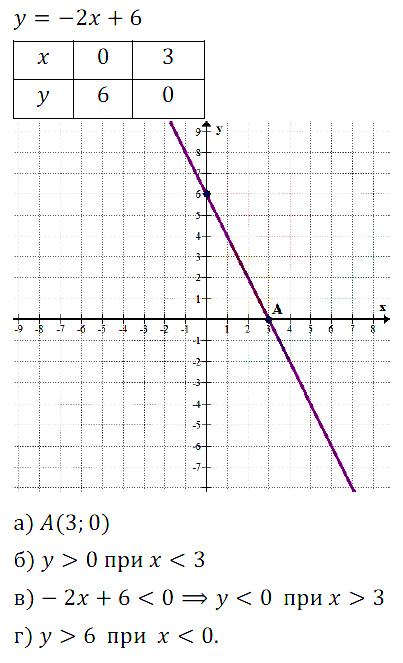
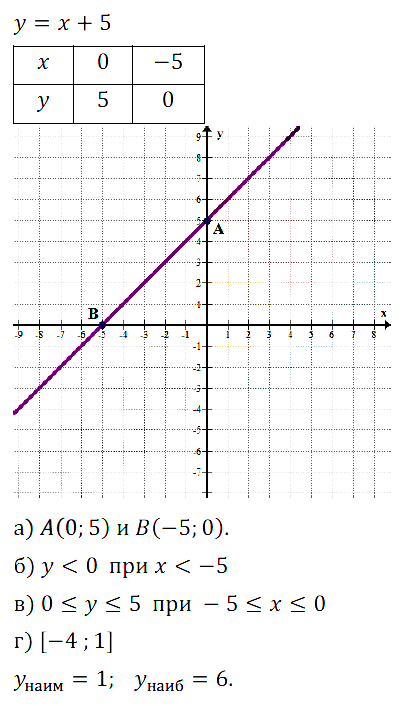
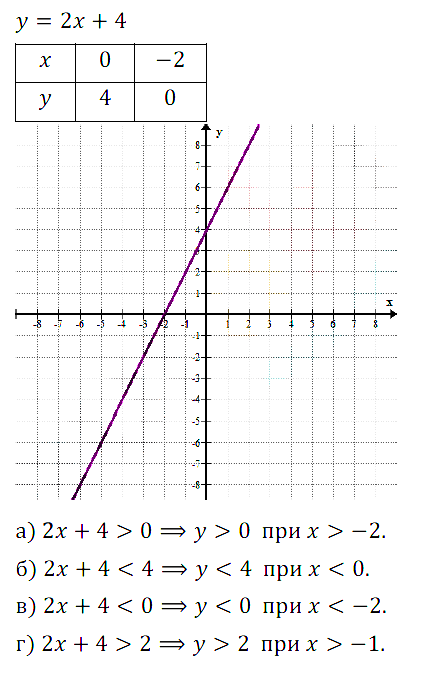
Не помагают. Ответы есть и вроде правильные, но не понятно как пришли к тому или иному ответу