Алгебра 7 класс УМК Мерзляк, Поляков (угл.) онлайн. Глава 3. Функции (§23 — §27). § 23 Множество и его элементы. § 24 Связи между величинами. Функция. § 25 Способы задания функции. § 26 График функции. § 27 Линейная функция, её график и свойства.
Алгебра 7 класс Мерзляк, Поляков (угл.изуч.)
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Глава 3. Функции (§23-§27)
В этой главе вы будете изучать связи между величинами. Познакомитесь с особым правилом, определяющим эти связи, — функцией. Изучите основные способы задания функции.
§ 23 Множество и его элементы
Рассмотрим словосочетания: косяк рыб, стая птиц, рой пчёл, коллекция марок, собрание картин, набор ручек, букет цветов, компания друзей, парк машин, отара овец.
Из слов этих словосочетаний можно составить новые: например, букет баранов, косяк картин, коллекция друзей, но они получились нелепыми. В то же время такие словосочетания, как коллекция рыб, коллекция птиц, коллекция картин, коллекция ручек, коллекция машин, имеют смысл. Дело в том, что слово «коллекция» универсальное. Однако в математике есть более ёмкое слово, которым можно заменить любое из первых слов в приведённых парах. Это слово множество.
Приведём ещё несколько примеров множеств:
• множество учеников вашего класса;
• множество планет Солнечной системы;
• множество чётных чисел;
• множество точек, лежащих на одной прямой;
• множество натуральных чисел, которое обозначают буквой N.
Как правило, множества обозначают прописными латинскими буквами: А, В, С, D и т. д.
Объекты, составляющие данное множество, называют элементами этого множества. Обычно элементы обозначают строчными латинскими буквами: а, b, с, d и т. д.
§ 24 Связи между величинами. Функция
Учитель пишет на доске. При этом меняются длина мелового следа, масса, объём и даже температура кусочка мела.
Работает школьная столовая. В течение дня меняются количество посетивших её учеников, расходы электроэнергии и воды, денежная выручка и т. п.
Вообще, в происходящих вокруг нас процессах многие величины меняют свои значения. Понятно, что некоторые из этих величин связаны между собой, т. е. изменение одной величины влечёт за собой изменение другой.
Многие науки, такие как физика, химия, биология и др., исследуют зависимости между величинами. Изучает эти связи и математика, конструируя математические модели реальных процессов. С понятием математической модели вы уже встречались в § 3.
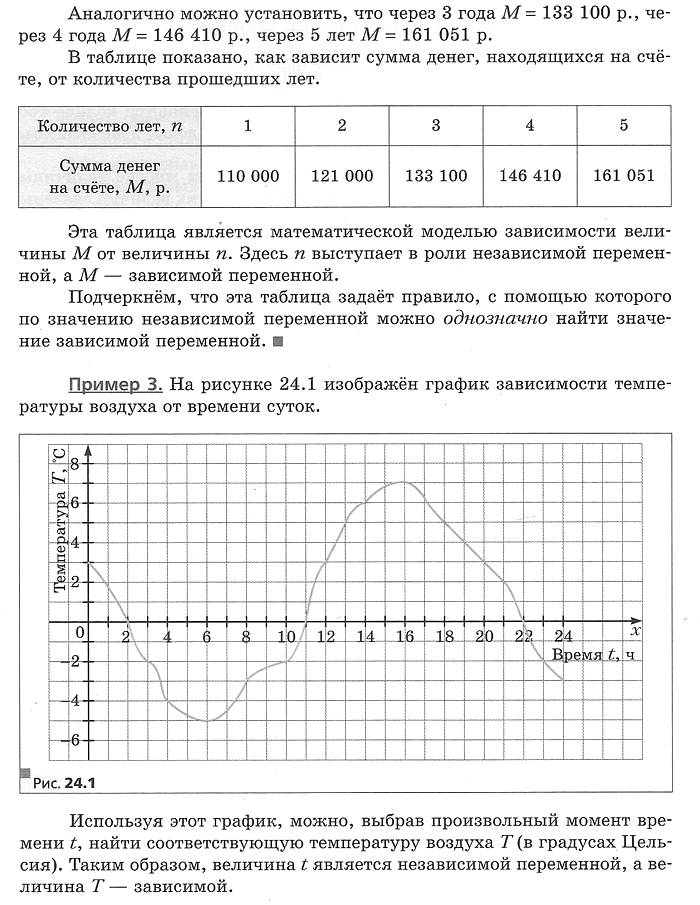
Рассмотрим несколько примеров.
§ 25 Способы задания функции
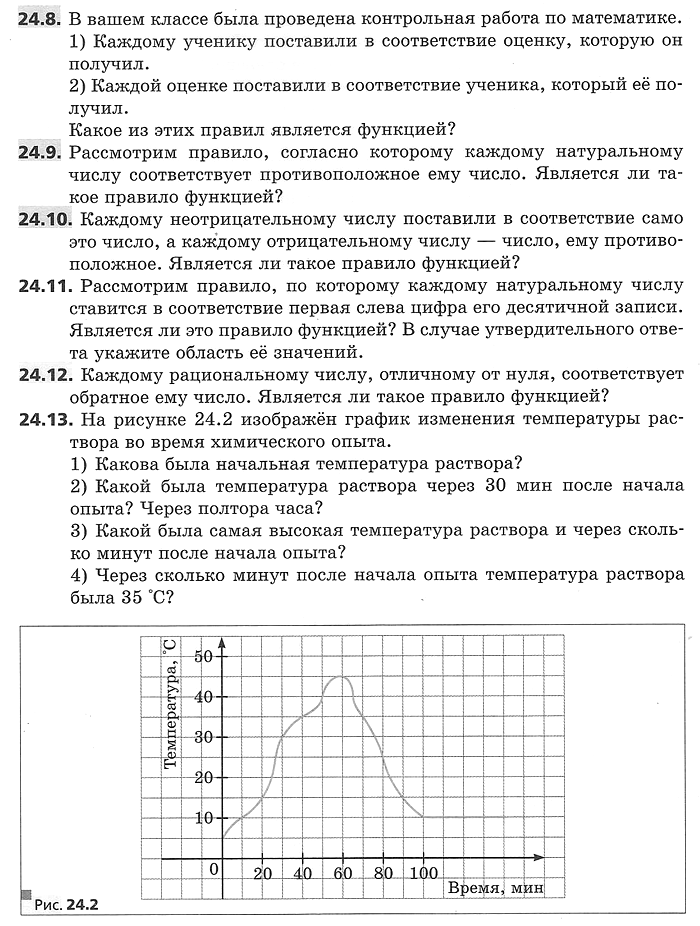
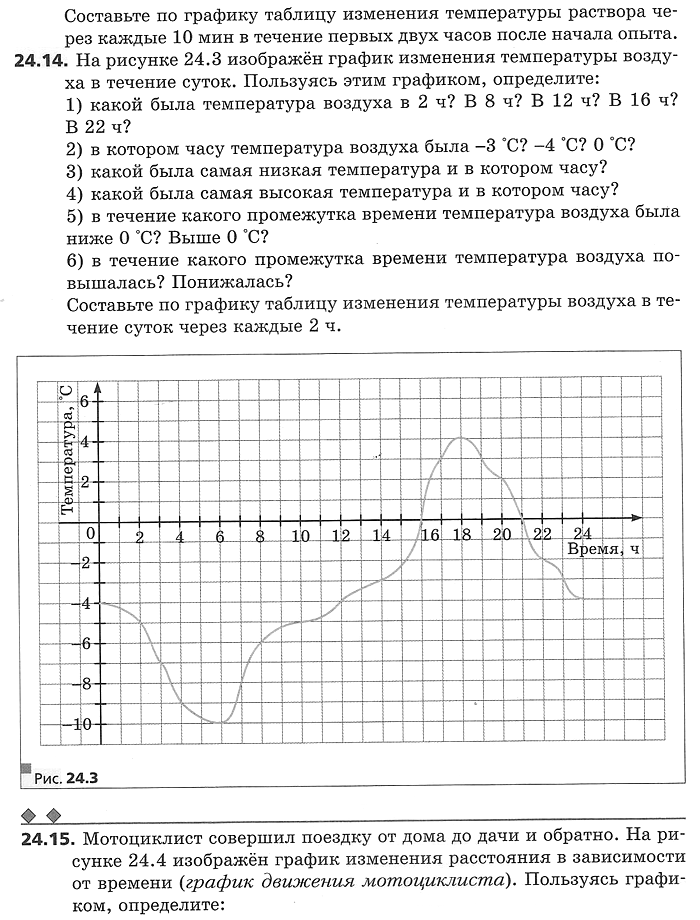
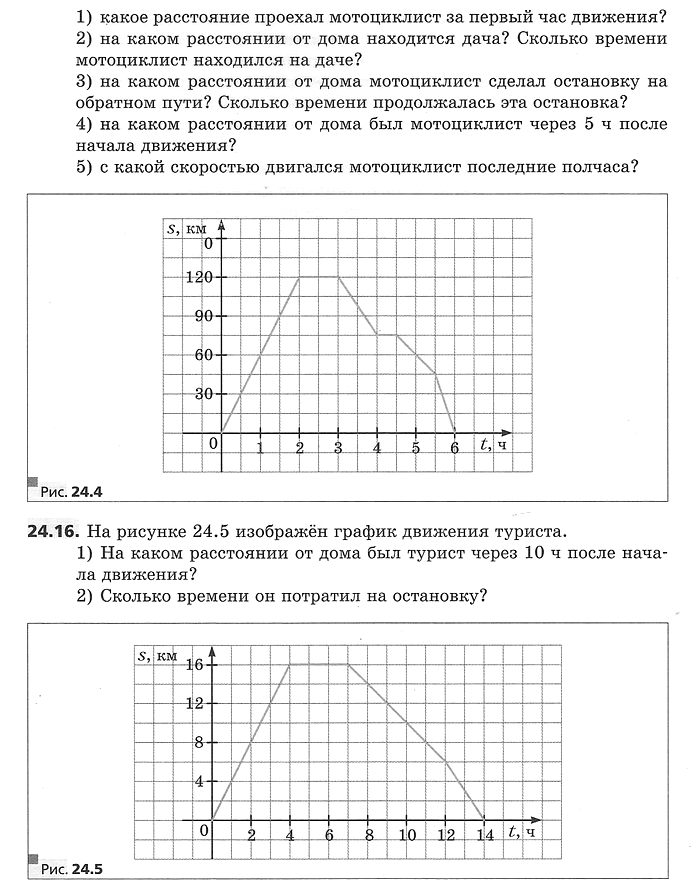
Примеры, рассмотренные в предыдущем параграфё, показывают, что функцию можно задавать различными способами.
Функция считается заданной, если указаны её область определения и правило, с помощью которого можно по каждому значению независимой переменной найти значение зависимой переменной.
Вам не раз приходилось формулировать различные правила. Поскольку функция — это правило, то её можно задать словами. Такой способ задания функции называют описательным.
Приведём несколько примеров.
§ 26 График функции
§ 27 Линейная функция, её график и свойства
Итоги главы 3
Равные множества
Множества А и В называют равными, если они состоят из одних и тех же элементов, т. е. каждый элемент множества А принадлежит множеству В и наоборот — каждый элемент множества В принадлежит множеству А.
Функция
Функцией называют правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной из множества Y.
Область определения функции
Все значения аргумента образуют множество, которое называют областью определения функции.
Область значений функции
Все значения зависимой переменной образуют множество, которое называют областью значений функции.
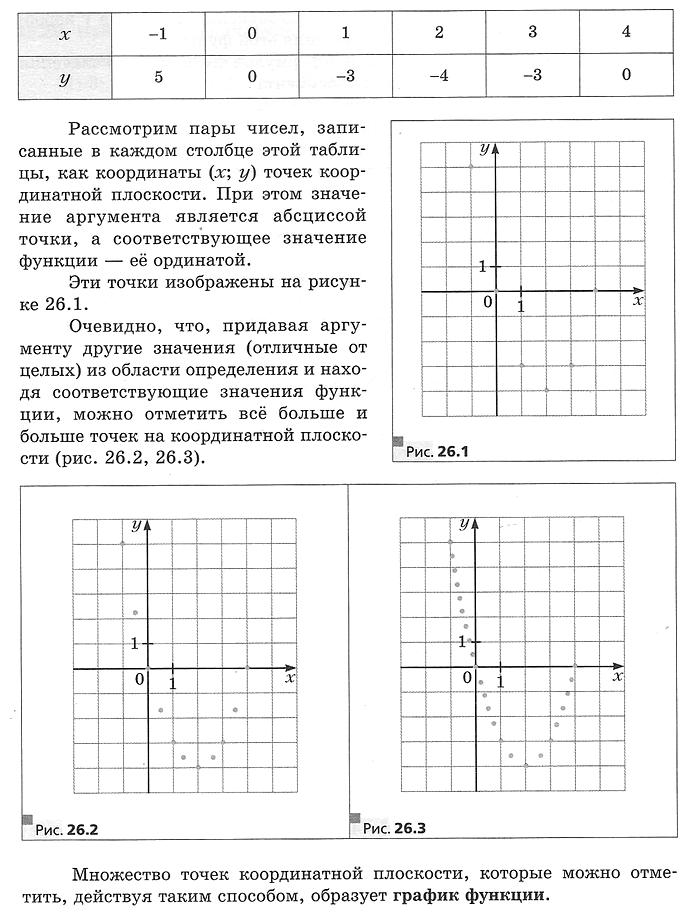
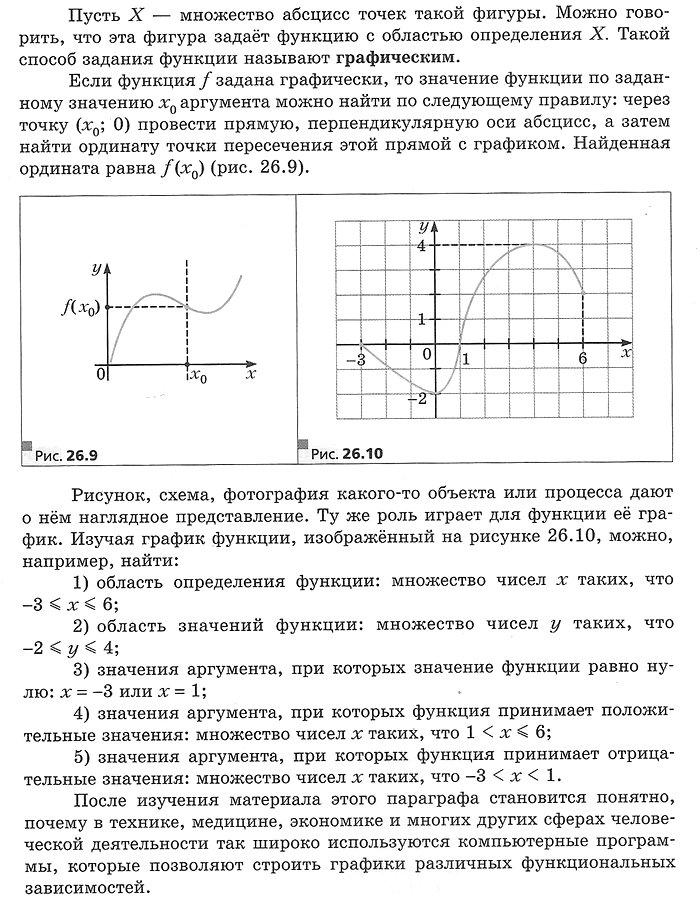
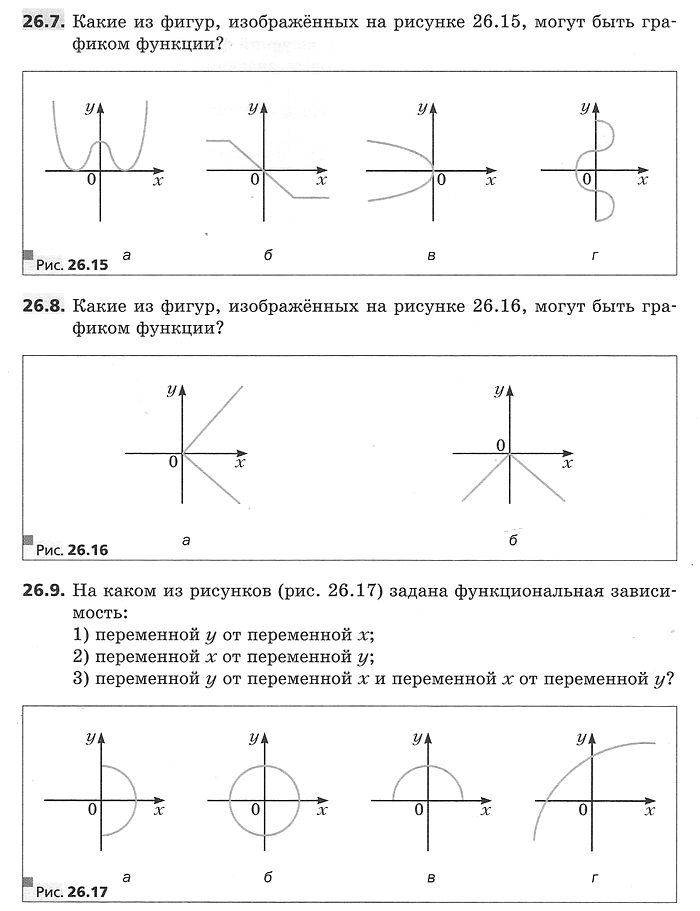
График функции
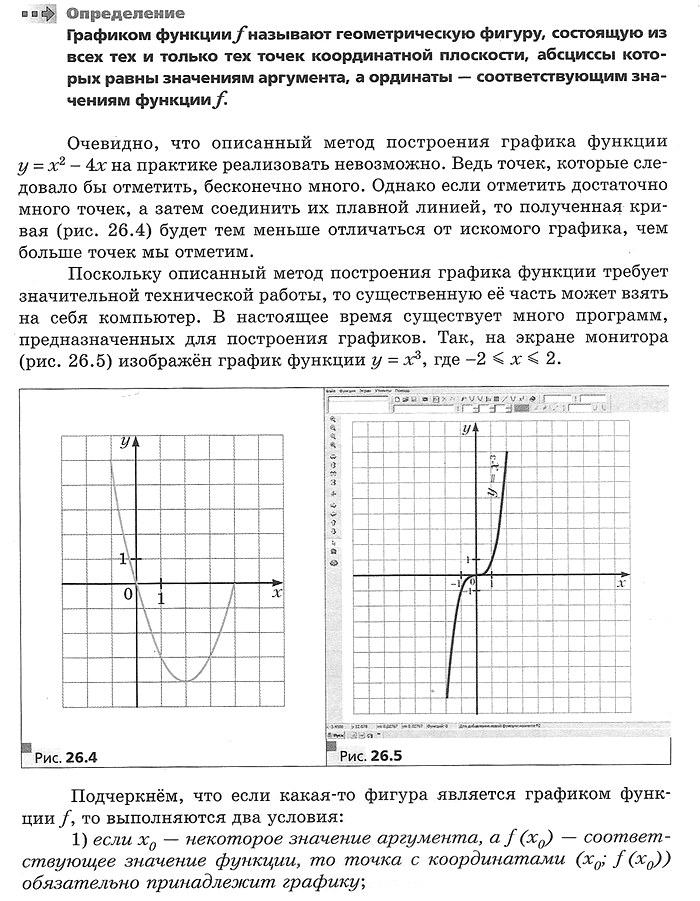
Графиком функции f называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции f.
Линейная функция
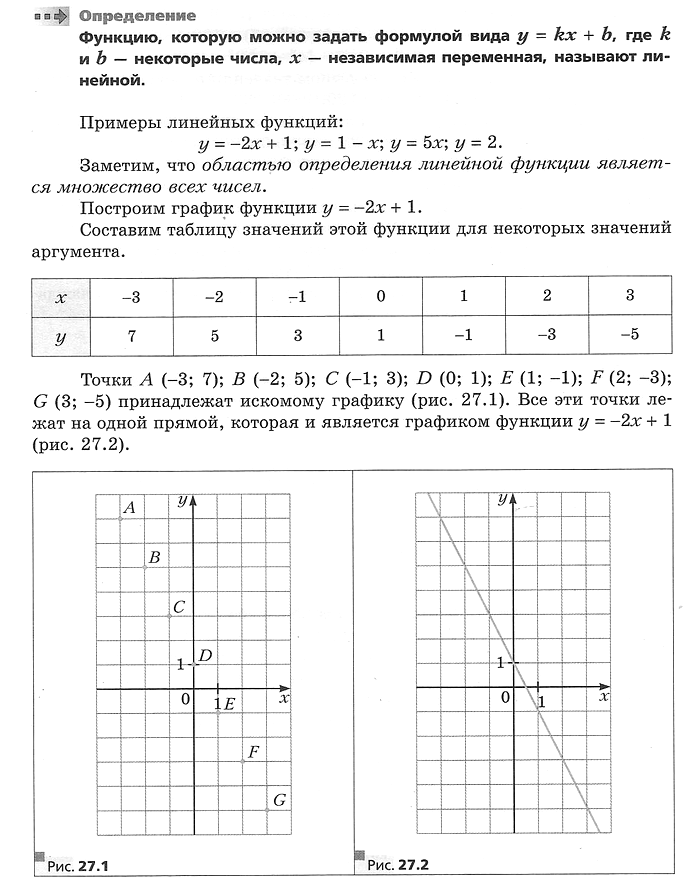
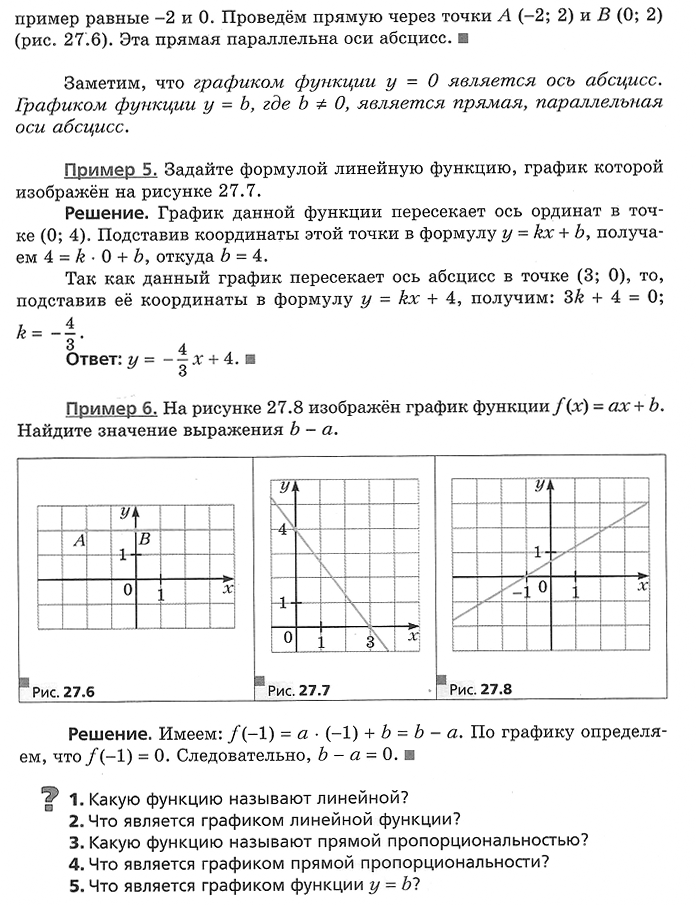
Функцию, которую можно задать формулой вида у = kx + b, где k и b — некоторые числа, х — независимая переменная, называют линейной.
График линейной функции
Графиком линейной функции является прямая.
Прямая пропорциональность
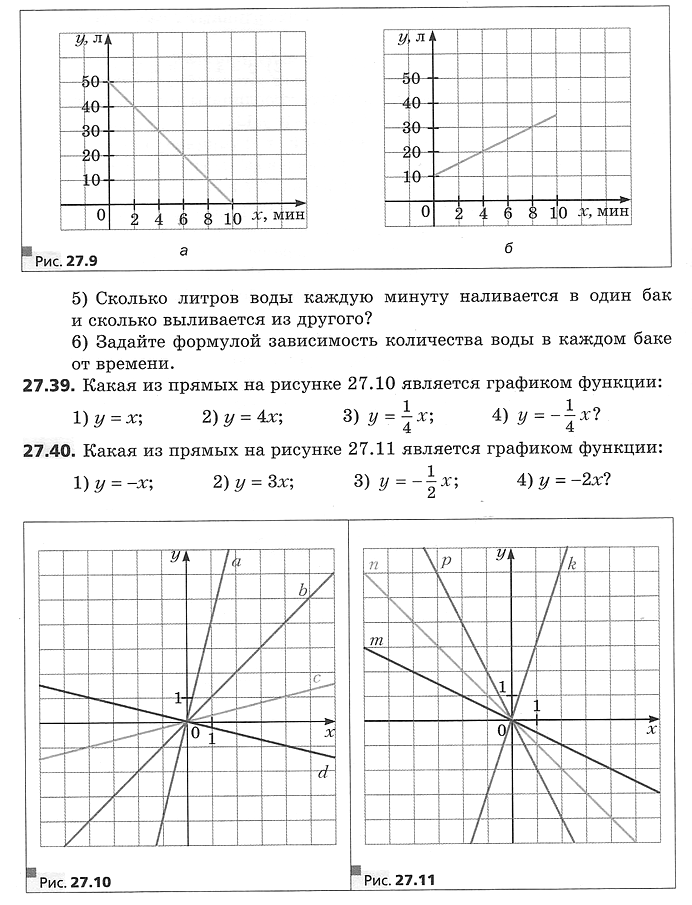
Линейную функцию, которую задают формулой у = kx, где k ≠ 0, называют прямой пропорциональностью.
Предыдущая тема ОГЛАВЛЕНИЕ Следующая тема
Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф (Российский учебник). Глава 3. Функции (§23 — §27). § 23 Множество и его элементы. § 24 Связи между величинами. Функция. § 25 Способы задания функции. § 26 График функции. § 27 Линейная функция, её график и свойства.